Question

15．如图1，等腰△ABC中，AB=BC，AD⊥BC于D，点E在边AB上，EF⊥AC于F，EF交AD于G点．
（1）求证：∠AEF=$\frac{1}{2}$∠ABC；
（2）当∠ABC=45°时，求证：EG=2AF；
（3）如图2，当EG=AF时，求$\frac{{S}_{△ACD}}{{S}_{△ABD}}$的值．

Answer 1

分析 （1）作BM⊥AC垂足为M，根据三线合一、平行线的性质即可得证．
（2）过点E作EM∥BC，分别交AD、AC于点N、M，先证明△AEN是等腰直角三角形，再证明△ENG≌△ANM，得到BG=AM，最后证明△EMA为等腰三角形，即可解答．
（3）根据△ENG∽△ANM得$\frac{EG}{AM}=\frac{EN}{NA}$=$\frac{1}{2}$由EN∥BD得$\frac{EN}{BD}=\frac{AN}{AD}$所以$\frac{BD}{AD}=\frac{EN}{AN}=\frac{1}{2}$，设BD=a，则AD=2a，AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{5}a$，求出CD，根据$\frac{{S}_{△ACD}}{{S}_{△ABD}}$=$\frac{CD}{BD}$即可解决．

解答 （1）证明：如图1中，作BM⊥AC垂足为M，∵EF⊥AC，BM⊥AC，
∴BM∥EF，
∴∠AEF=∠ABM，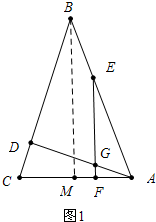
∵BC=BA，BM⊥AC，
∴∠ABM=∠CBM=$\frac{1}{2}$∠ABC，
∴∠AEF=$\frac{1}{2}$∠ABC．
（2）证明：如图2中，过点E作EM∥BC，分别交AD、AC于点N、M，
∵EM∥BC，
∴∠MEA=∠B=45°，∠ENA=∠ADB=90°，
∴△AEN为等腰直角三角形，
∴NE=NA，
∴∠ENA=∠ANM，
∵EF⊥AC，
∴∠EFA=90°，
∴∠ENA=∠EFA，
又∵∠EGN=∠AGF，
∴180°-∠ENA-∠EGM=180°-∠EFA-∠AGF，
即∠NEG=∠NAM，
在△ENG与△ANM中，
$\left\{\begin{array}{l}{∠ENA=∠ANM}\\{EN=NA}\\{∠NEG=∠NAM}\end{array}\right.$，
∴△ENG≌△ANM，
∴EG=AM，
∵BC=BA，
∴∠C=∠BAC，
∵EM∥BC，
∴∠EMA=∠C，
∴∠EMA=∠BAC，
∴△EMA为等腰三角形，
∵EF⊥MA，
∴AM=2AF，
∴EG=2AF．
（3）如图2中，作EM∥BC交AD于N，
∵BC=BA，
∴∠C=∠BAC，
∵EM∥BC，
∴∠EMA=∠C，
∴∠EMA=∠BAC，
∴△EMA为等腰三角形，
∵EF⊥MA，
∴AM=2AF=2EG，
∵AD⊥BC，
∴EM⊥AD，
∵EF⊥AC，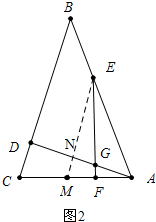
∴∠ENG=∠EFA=90°，
∵∠ENG=∠MNA，
∴△ENG∽△ANM，
∴$\frac{EG}{AM}=\frac{EN}{NA}$=$\frac{1}{2}$，
∵EN∥BD，
∴$\frac{EN}{BD}=\frac{AN}{AD}$，
∴$\frac{BD}{AD}=\frac{EN}{AN}=\frac{1}{2}$，
设BD=a，则AD=2a，AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=$\sqrt{5}a$，
∴BC=BA=$\sqrt{5}$a，
CD=$\sqrt{5}$a-a，
∴$\frac{{S}_{△ACD}}{{S}_{△ABD}}$=$\frac{CD}{BD}$=$\frac{\sqrt{5}a-a}{a}$=$\sqrt{5}$-1．

点评 本题考查了全等三角形的性质和判定定理、等腰三角形的性质，解决本题的关键是作辅助线，构建三角形全等，通过设未知数列出相应的代数式，把面积比变成线段比．