
【题目】如图,Rt△ABC中,∠ABC=90°以AB为直径的⊙O交AB于点D,点E为BC的中点,连接DE.
(1)求证:DE是⊙O的切线.
(2)若∠BAC=30°,DE=3,求AD的长.
【答案】
(1)证明:连接OD、BD,
∵AB为⊙O的直径,
∴∠ADB=∠CDB=90°;
又∵点E为BC的中点,
∴BE=DE,
∴∠BDE=∠EBD;
∵OA=OD,
∴∠OAD=∠ODA;
又∵∠OAD+∠OBD=90°,∠EBD+∠OBD=90°,
∴∠OAD=∠EBD,即∠ODA=∠BDE;
∴∠ODE=∠BDE+∠ODB=∠ODA+∠ODB=90°,
又∵点D在⊙O上,
∴DE是圆⊙O的切线.
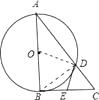
(2)解:由(1)知BC=2DE=6,
又∵∠CBD=∠BAC=30°,
∴CD=3,BD=3 ![]()
∴AB=6 ![]() ;
;
由勾股定理得:AD=9.
【解析】(1)连接OD、BD,由圆周角定理得∠ADB=∠CDB=90°;在直角三角形中,斜边上的中线等于斜边的一半,依此得BE=DE,再由等腰三角形的性质得 ∠BDE=∠EBD;∠OAD=∠ODA; 根据同角的余角相等和等量代换得∠ODA=∠BDE;由此得出∠ODE=90°,即DE是圆⊙O的切线.
(2)由(1)知BC=2DE=6,在直角三角形中,30°所对的直角边等于斜边的一半,即CD=3,根据勾股定理得BD=3 ![]() ,再由在直角三角形中,30°所对的直角边等于斜边的一半,得AB=6
,再由在直角三角形中,30°所对的直角边等于斜边的一半,得AB=6 ![]() ,由勾股定理得:AD=9.
,由勾股定理得:AD=9.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.
(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;
(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;
(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法﹣﹣更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也.以等数约之”,意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.
例如:求91与56的最大公约数
解:
请用以上方法解决下列问题:
(1)求108与45的最大公约数;
(2)求三个数78、104、143的最大公约数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,途中小凡从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程![]() (千米)与时间
(千米)与时间![]() (分钟)的关系,请根据图象提供的信息回答问题:
(分钟)的关系,请根据图象提供的信息回答问题:

(1)![]() 和
和![]() 中,__________描述小凡的运过程.
中,__________描述小凡的运过程.
(2)___________谁先出发,先出发了___________分钟.
(3)___________先到达图书馆,先到了____________分钟.
(4)当![]() _________分钟时,小凡与小光在去学校的路上相遇.
_________分钟时,小凡与小光在去学校的路上相遇.
(5)小凡与小光从学校到图书馆的平均速度各是多少千米/小时?(不包括中间停留的时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2AD,点E、F分别是AB、BC边的中点,连接AF、CE交于点M,连接BM并延长交CD于点N,连接DE交AF于点P,则结论:①∠ABN=∠CBN;②DE∥BN;③△CDE是等腰三角形;④EM:BE= ![]() :3;⑤S△EPM=
:3;⑤S△EPM= ![]() S梯形ABCD , 正确的个数有( )
S梯形ABCD , 正确的个数有( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请先阅读下列文字与例题,再回答后面的问题:
当因式分解中,无法直接运用提取公因式和乘法公式时,我们往往可以尝试一个多项式分组后,再运用提取公因式或乘法公式继续分解的方法是分组分解法.
例如:
(1)![]()
=![]()
=![]()
=![]()
(2)![]()
=![]()
=![]()
=![]()
(1)根据上面的知识,我们可以将下列多项式进行因式分解:
![]() (_____________)-(____________)=(_____________)-(____________)= (_____________)(_____________);
(_____________)-(____________)=(_____________)-(____________)= (_____________)(_____________);
![]() =(_____________)+(____________)=(_____________)+(____________)= (_____________)(______________).
=(_____________)+(____________)=(_____________)+(____________)= (_____________)(______________).
(2)分解下列因式:
①![]() ;
;
②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
A.20海里
B.10 ![]() 海里
海里
C.20 ![]() 海里
海里
D.30海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() ,点
,点![]() ,
, ![]() 分别是射线
分别是射线![]() ,
, ![]() 上两定点,且
上两定点,且![]() ,
, ![]() ;动点
;动点![]() 从点
从点![]() 向点
向点![]() 运动,以
运动,以![]() 为斜边向右侧作等腰直角
为斜边向右侧作等腰直角![]() .设线段
.设线段![]() 的长
的长![]() ,点
,点![]() 到射线
到射线![]() 的距离为
的距离为![]() .
.
(1)若![]() ,直接写出点
,直接写出点![]() 到射线
到射线![]() 的距离;
的距离;
(2)求![]() 关于
关于![]() 的函数表达式,并在图
的函数表达式,并在图![]() 中画出函数图象;
中画出函数图象;
(3)当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,求点
,求点![]() 运动经过的路径长.
运动经过的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com