
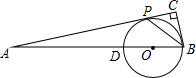
 如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.
如图,在△ABC中,∠ACB=90°,点P是AC上一点,且BP平分∠ABC,点D是AB上一点,以BD为直径的⊙O经过点P.分析 (1)连结OP,如图,由BP平分∠ABC得∠CBP=∠OBP,由OB=OP得∠OBP=∠OPB,则∠CBP=∠OPB,根据平行线的判定得OP∥BC,则利用平行线的性质得到∠APO=∠C=90°,于是可根据切线的判定定理得到结论;
(2)根据三角形面积公式由△ABP的面积-△BPC的面积=2可得BC(PA-1)=4,即BC=$\frac{4}{PA-1}$,再根据平行线分线段成比例定理可推出$\frac{PA}{PC}$=$\frac{AB}{BC}$,则AB=PA•BC,接着利用勾股定理有AB2=AC2+BC2,所以PA2•BC2=(AP+1)2+BC2,移项变形得到(AP+1)2=BC2(PA2-1),所以PA+1=BC2(PA-1),然后把BC=$\frac{4}{PA-1}$代入得到关于PA的方程,然后解方程即可.
解答 (1)证明 :连结OP,如图,
:连结OP,如图,
∵BP平分∠ABC,
∴∠CBP=∠OBP,
∵OB=OP,
∴∠OBP=∠OPB,
∴∠CBP=∠OPB,
∴OP∥BC,
∴∠APO=∠C=90°,
∴OP⊥AP,
∴AC是⊙O的切线;
(2)解:∵△ABP的面积-△BPC的面积=2,PC=1,
∴$\frac{1}{2}$AP•BC-$\frac{1}{2}$PC•BC=2,
∴BC(PA-1)=4,
∴BC=$\frac{4}{PA-1}$
∵OP∥BC,
∴$\frac{AO}{AB}$=$\frac{OP}{BC}$,$\frac{AP}{PC}$=$\frac{AO}{OB}$
∴$\frac{AO}{OP}$=$\frac{AB}{BC}$,
而OP=OB,
∴$\frac{PA}{PC}$=$\frac{AB}{BC}$,则AB=PA•BC,
∵AB2=AC2+BC2,
∴PA2•BC2=(AP+1)2+BC2,
∴(AP+1)2=BC2(PA2-1),
∴PA+1=BC2(PA-1),
∴PA+1=($\frac{4}{PA-1}$)2•(PA-1),
∴PA=$\sqrt{17}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行线分线段成比例定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
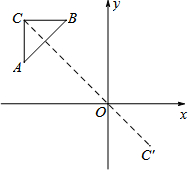 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,-3) | B. | (2,-1) | C. | (3,-2) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
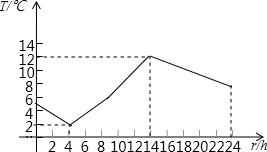 如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )| A. | 10℃ | B. | -10℃ | C. | 8℃ | D. | 12℃ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com