练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
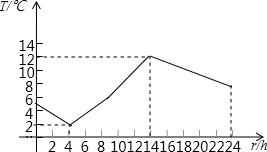
    10．如图是自动温度计记录的某一天气温变化的曲线，它反映了变量T（℃）与t（h）之间的对应关系，这一天中，温差（最高与最低温度的差）是（　　）
    A．10℃B．-10℃C．8℃D．12℃

    分析 观察函数图象，可得最高温度、最低温度，根据有理数的减法，可得答案．

    解答 解：由纵坐标看出最高温度是12℃，最低温度是2°，
    由有理数的减法，得
    12-2=10℃，
    故选：A．

    点评 本题考查了函数图象，观察函数图象得出最高温度、最低温度是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

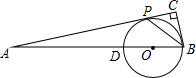    4．如图，在△ABC中，∠ACB=90°，点P是AC上一点，且BP平分∠ABC，点D是AB上一点，以BD为直径的⊙O经过点P．
    （1）求证：AC是⊙O的切线；
    （1）若△ABP的面积-△BPC的面积=2，PC=1，求PA的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图中直线l1，l2被l3所截，则同位角有（　　）对．
    A．1对B．2对C．3对D．4对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．在梯形ABCD中，AD∥BC，对角线AC⊥BD于O，BD=3，AC=4．求梯形的高和面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知：如图1，在平面直角坐标系xOy中，直线y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$与x轴，y轴的交点分别为A，B，将∠OBA对折，折痕交x轴于点C，一过点B的抛物线顶点恰好在点C．
    （1）直接写出点C的坐标，并求出抛物线的解析式：
    （2）Q为线段BC上一点，请求出|QA-QO|的取值范围；
    （3）在x轴上有一点D（1，0），连接BD，在△BCD中有一点E，E点到△BCD各顶点的距离相等，直线DE交抛物线的对称轴于点F．
    ①在图2中作出点E和点F，并求出点E的坐标；
    ②当x＞-1时，在直线CE和抛物线上是否分别存在点M和点N，使四边形FCMN为特殊梯形？若存在，求点M，N的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

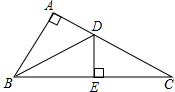    15．如图，已知Rt△ABC中，AB=AC、BC=10，∠A为Rt∠，BD为△ABC的一条角平分线，过点D作DE垂直于BC，求△CDE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．一辆汽车的油箱中装满200升汽油，1升汽油可使汽车行驶5千米．
    （1）求油箱的余油量Q（升）与行驶路程S（千米）之间的关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解答题 
    （1）如图1，线段MN=30cm，MO=GO=3cm，点P从点M开始绕着点O以15°/s的速度顺时针旋转一周回到点M后停止，点Q同时出发沿射线NM自N点向M点运动，若点P、Q两点能恰好相遇，则点Q运动的速度为1.25或2cm/s．

    （2）要使（x2+mx+8）（x2-3x+n）的展开式中不含x3项和x2项，求m，n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

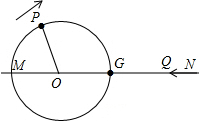
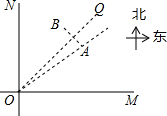    20．如图，某城市中心的两条公路OM和ON，其中OM为东西走向，ON为南北走向，A、B是两条公路所围区域内的两个标志性建筑．已知A、B关于∠MON的平分线OQ对称．OA=1000米，测得建筑物A在公路交叉口O的北偏东53.5°方向上．
    求：建筑物B到公路ON的距离．
    （参考数据：sin53.5°=0.8，cos53.5°=0.6，tan53.5°≈1.35）

    查看答案和解析>>

    同步练习册答案