
分析 过D作DE∥AC交BC延长线于E,得到四边形ACED是平行四边形和直角△BDE,根据面积公式求出高,根据等底同高的两个三角形面积相等,求出△BDE的面积,得到梯形的面积.
解答 解:过D作DE∥AC交BC延长线于E,
∵AD∥BC,DE∥AC,
∴四边形ACED是平行四边形,
∴AD=CE,DE=AC=4,
∠BDE=∠BOC=90°,
BD=3,DE=4,根据勾股定理,BE=5,
设梯形的高为h,
则$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×h,
h=$\frac{12}{5}$,
∵AD=CE,
∴△ADB的面积=△DCE的面积,
则梯形的面积=△BDE的面积=6.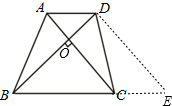
点评 本题考查的是梯形的性质和有关计算,正确作出辅助线是解题的关键,注意,等底同高的两个三角形面积相等.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
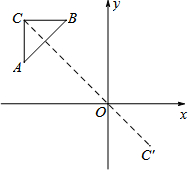 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,-3) | B. | (2,-1) | C. | (3,-2) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
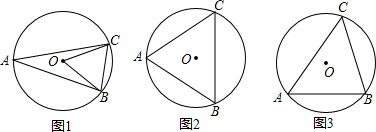
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
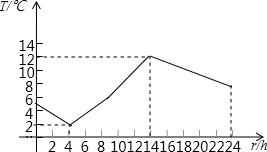 如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )
如图是自动温度计记录的某一天气温变化的曲线,它反映了变量T(℃)与t(h)之间的对应关系,这一天中,温差(最高与最低温度的差)是( )| A. | 10℃ | B. | -10℃ | C. | 8℃ | D. | 12℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
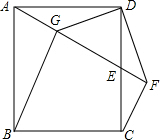 如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.
如图,已知在正方形ABCD中,点E在CD边长,过C点作AE的垂线交于点F,联结DF,过点D作DF的垂线交A于点G,联结BG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com