练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2018个格子中的整数是_______．

    【答案】6

    【解析】

    根据三个相邻格子的整数的和相等列式求出a、c的值，再根据第9个数是-2可得b=-2，然后找出格子中的数每3个为一个循环组依次循环，在用2018除以3，根据余数的情况确定与第几个数相同即可得解．

    ∵任意三个相邻格子中所填整数之和都相等，
    ∴2+a+b=a+b+c，
    解得c=2，
    a+b+c=b+c+6，
    解得a=6，
    所以，数据从左到右依次为2、6、b、2、6、b，
    第9个数与第三个数相同，即b=-2，
    所以，每3个数“2、6、-2”为一个循环组依次循环，
    ∵2018÷3=672……2，
    ∴第2018个格子中的整数与第2个格子中的数相同，为6．
    故答案为：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC中，∠A=90°．

    （1）请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切（保留作图痕迹，不写作法和证明）；

    （2）在（1）的条件下，若∠B=45°，AB=1，⊙P切BC于点D，求劣弧的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

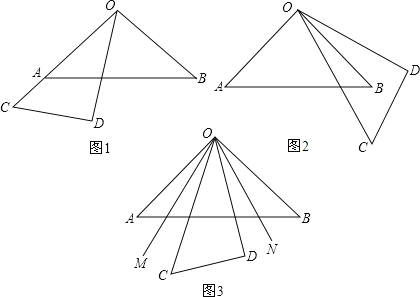
    【题目】已知将一副三角板（直角三角板OAB和直角三角板OCD，∠AOB＝90°，∠COD＝30°）如图1摆放，点O、A、C在一条直线上．将直角三角板OCD绕点O逆时针方向转动，变化摆放如图位置

    （1）如图1，当点O、A、C在同一条直线上时，则∠BOD的度数是多少？

    （2）如图2，若要OB恰好平分∠COD，则∠AOC的度数是多少？

    （3）如图3，当三角板OCD摆放在∠AOB内部时，作射线OM平分∠AOC，射线ON平分∠BOD，如果三角板OCD在∠AOB内绕点O任意转动，∠MON的度数是否发生变化？如果不变，求其值；如果变化，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两家商场同时出售同样的水瓶和水杯，且定价相同，请根据图中提供的信息，回答下列问题：

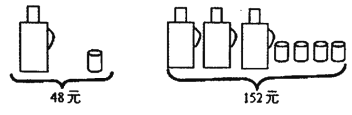
    (1)一个水瓶与一个水杯分别是多少元?(请列方程解应用题)

    (2)为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打八折；乙商场规定：买一个水瓶赠送两个水杯，另外购买的水杯按原价卖.若某单位想要买5个水瓶和12个水杯，请问选择哪家商场购买更合算，并说明理由(水瓶和水杯必须在同一家购买).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（大丰某校数学兴趣小组活动场景）

    （课堂再现）

    师：同学们还记得教材P43分配律a（b+c）=ab+ac吗？现在，老师和大家一起来用几何的方法来证明这个公式。相信今天会惊喜不断。（学生期待惊喜中………），

    （教者呈现教具）老师手上有两个长方形，长分别是b、c，宽都是a，（如图1）它们各自面积是多少？

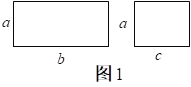
    生1：面积分别为ab、ac。

    师：现在我们把它们拼在一起（如图2），组成了一个新长方形，新长方形面积又是多少呢？

    生2：

    师：所以……

    生3：所以得到，也就是说（真好玩！）

    师：相信大家能用类似方法来推导一个我们暂时还没学习的公式，老师期待大家给我的惊喜哦！（屏幕上呈现问题）

    （拓展延伸）

    将边长为a的正方形纸板上剪去一个边长为b的正方形（如图3），将剩余的纸板沿虚线剪开，拼成如图4的梯形。

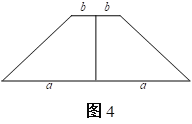
    （1）你能得到一个什么等式.（用含a、b的式子表示）

    （再接再厉）

    （2）直接运用上面你发现的公式完成运算：

    （拓展提高）

    （3）直接运用上面你发现的公式解下列方程：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是由若干个完全相同的小正方体组成的一个几何体。

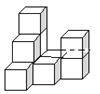
    （1）图中有　 　块小正方体；

    （2）请画出这个几何体的左视图和俯视图；（用阴影表示）

    （3）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的俯视图和左视图不变，那么最多可以再添加几个小正方体？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）

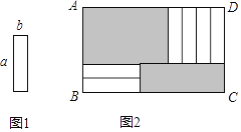
    A. a=2b B. a=3b C. a=4b D. a=b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人利用不同的交通工具，沿同一路线分别从A、B两地同时出发匀速前往C地（B在A、C两地的途中）．设甲、乙两车距A地的路程分别为y甲、y乙（千米），行驶的时间为x（小时），y甲、y乙与x之间的函数图象如图所示．

    （1）直接写出y甲、y乙与x之间的函数表达式；

    （2）如图，过点（1，0）作x轴的垂线，分别交y甲、y乙的图象于点M，N．求线段MN的长，并解释线段MN的实际意义；

    （3）在乙行驶的过程中，当甲、乙两人距A地的路程差小于30千米时，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分类讨论是一种非常重要的数学方法，如果一道题提供的已知条件中包含几种情况，我们可以分情况讨论来求解.例如：已知点A，B，C在一条直线上，若AB=8，BC=3则AC长为多少？

    通过分析我们发现，满足题意的情况有两种：情况当点C在点B的右侧时，如图1，此时，AC=11；

    情况②当点C在点B的左侧时， 如图2此时，AC=5.

    仿照上面的解题思路，完成下列问题:

    问题（1）: 如图,数轴上点A和点B表示的数分别是-1和2，点C是数轴上一点，且BC=2AB，则点C表示的数是.

    问题(2): 若，求的值.

    问题(3): 点O是直线AB上一点，以O为端点作射线OC、OD，使，，求的度数（画出图形，直接写出结果）.

    查看答案和解析>>

    同步练习册答案