
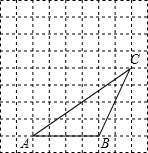
 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.分析 (1)首先确定A、B、C三点平移后的位置,再顺次连接即可;
(2)根据平移的性质:对应点连线平行且相等可得AA′=CC′,AA′∥CC;
(3)根据三角形的中线平分三角形的面积可得MN就是△ABC中线所在直线,因此根据网格图可得AB的中点位置,再画直线即可.
解答 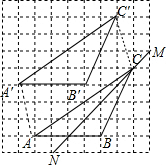 解:(1)如图所示:
解:(1)如图所示:
(2)连接AA′,CC′,根据平移的性质可得AA′=CC′,AA′∥CC,
故答案为:平行且相等;
(3)如图所示.
点评 本题考查的是平移变换作图以及平移的性质.作平移图形时,找关键点的对应点也是关键的一步.平移作图的一般步骤为:
①确定平移的方向和距离,先确定一组对应点;
②确定图形中的关键点;
③利用第一组对应点和平移的性质确定图中所有关键点的对应点;
④按原图形顺序依次连接对应点,所得到的图形即为平移后的图形.


科目:初中数学 来源: 题型:选择题
| A. | x$\sqrt{-2x}$ | B. | -x$\sqrt{-2x}$ | C. | -$\sqrt{2x^3}$ | D. | x2$\sqrt{-\frac{2}{x}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
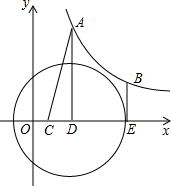 如图所示:点A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两个动点,分别过点A、B点作AD⊥x轴于D,BE⊥x轴于E,点C是线段OD的中点.
如图所示:点A,B是反比例函数y=$\frac{k}{x}$(x>0)图象上的两个动点,分别过点A、B点作AD⊥x轴于D,BE⊥x轴于E,点C是线段OD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com