
 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC等于8.
如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC、∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC等于8. 分析 作AH⊥BC于H,作直径CF,连结BF,先利用等角的补角相等得到∠DAE=∠BAF,然后再根据同圆中,相等的圆心角所对的弦相等得到DE=BF=6,由AH⊥BC,根据垂径定理得CH=BH,易得AH为△CBF的中位线,然后根据三角形中位线性质得到AH=$\frac{1}{2}$BF=3,再利用勾股定理,可求得BH的长,继而求得答案.
解答  解:作AH⊥BC于H,作直径CF,连结BF,如图,
解:作AH⊥BC于H,作直径CF,连结BF,如图,
∵∠BAC+∠EAD=180°,
而∠BAC+∠BAF=180°,
∴∠DAE=∠BAF,
∴$\widehat{DE}$=$\widehat{BF}$,
∴DE=BF=6,
∵AH⊥BC,
∴CH=BH,
∵CA=AF,
∴AH为△CBF的中位线,
∴AH=$\frac{1}{2}$BF=3.
∴BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BC=2BH=8.
故答案为:8.
点评 此题考查了圆周角定理、垂径定理、三角形中位线的性质以及勾股定理.注意掌握辅助线的作法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
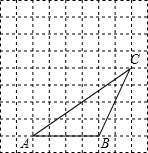 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
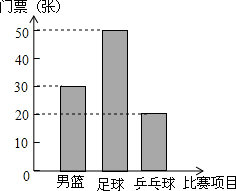 下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:
下表为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,某公司购买的门票种类、数量水质的统计图表如下:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
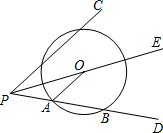 如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.
如图,射线PE平分∠CPD,O为射线PE上一点,以O为圆心作⊙O,与PD边交于点A、点B,连结OA,且OA∥PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
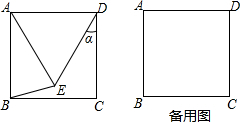
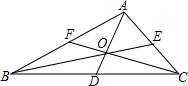 如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长.
如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
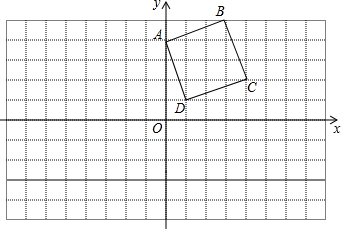 正方形ABCD在直角坐标系中的位置如图所示:
正方形ABCD在直角坐标系中的位置如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com