
【题目】沅陵一中有360张旧棵桌需维修,经过甲、乙两个维修小组的竞标得知,甲组工作效率是乙组的1.5倍,且甲组单独维修完这批旧课桌比乙组单独维修完这批旧课桌少用5天;已知甲组每天需要付工资800元,乙组每天需要付工资400元;
(1)求甲、乙两个小组每天各维修多少张旧棵桌?
(2)学校维修这批旧课桌预算资金不超过7000元,时间不超过12天,请你帮学校算一算有几种维修方案(天数不足1天的按1天算);每种方案需要多少钱?
【答案】(1)甲每天维修60张旧课桌,乙每天维修40张旧课桌;(2)由甲单独负责,此时完成工作需要6天,需要费用为4800元,由乙单独负责,此时完成工作需要9天,需要费用为3600元.
【解析】
(1) 设乙小组每天维修x张旧课桌,根据甲组工作效率是乙组的1.5倍,甲组单独维修完这批旧课桌比乙组单独维修完这批旧课桌少用5天,列方程解答即可;
(2) 分别计算甲乙单独完成该项工作的天数,根据题意给出的条件即可判断每种方案需要多少钱?.
(1)设乙小组每天维修x张旧课桌,
∴甲小组每天维修1.5x张旧课桌,
根据题意可知:![]() =
=![]() ﹣5,
﹣5,
解得:x=40,
经检验,x=40是原分式方程的解,
答:甲每天维修60张旧课桌,乙每天维修40张旧课桌;
(2)由甲单独负责,此时完成工作需要![]() =6天,需要费用为6×800=4800元,
=6天,需要费用为6×800=4800元,
由乙单独负责,此时完成工作需要![]() =9天,需要费用为9×400=3600元.
=9天,需要费用为9×400=3600元.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A的平分线交BC于D,过点D作DE⊥AC,DF⊥AB,垂足为点E、F,下面四个结论中:①∠AEF=∠AFE;②AD垂直平分EF;③S△BFD:S△CED=BF:CE;④EF∥BC,正确的是( )
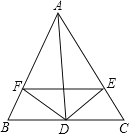
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
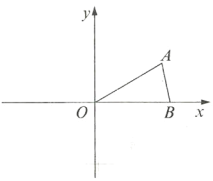
【题目】已知等腰![]() 在平面直角坐标系中的位置如图,点
在平面直角坐标系中的位置如图,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
(1)若将![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位,此时点
个单位,此时点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(2)若将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 恰好落在反比例函数
恰好落在反比例函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(3)若将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() 到
到![]() 位置,当点
位置,当点![]() 、
、![]() 恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点
恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点![]() 、
、![]() 且以
且以![]() 轴为对称的抛物线解析式.
轴为对称的抛物线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有A、B两种商品,已知在打折前,买60件A商品和30件B商品共用了1080元,买50件A商品和10件B商品共用了840元,A、B两种商品打相同折以后,某人买500件A商品和450件B商品一共花了7840元,请你计算A、B商品打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和等边△DBE,点D始终在射线AC上运动.
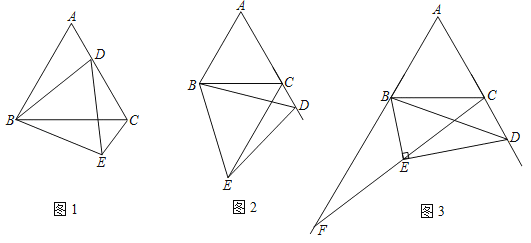
(1)如图1,当点D在AC边上时,连接CE,求证:AD=CE;
(2)如图2,当点D不在AC边上而在AC边的延长线上时,连接CE,(1)中的结论是否成立,并给予证明.
(3)如图3,当点D不在AC边上而在AC边的延长线上时,如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,BD 是 AC 边上的高,延长 BC 到 E使 CE=CD,则图中等腰三角形的个数是()

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com