
【题目】已知等边△ABC和等边△DBE,点D始终在射线AC上运动.
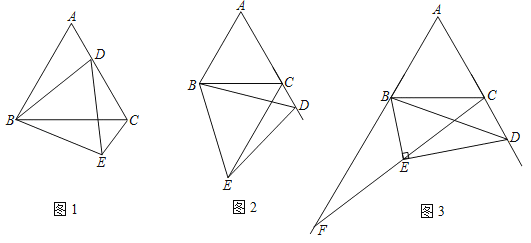
(1)如图1,当点D在AC边上时,连接CE,求证:AD=CE;
(2)如图2,当点D不在AC边上而在AC边的延长线上时,连接CE,(1)中的结论是否成立,并给予证明.
(3)如图3,当点D不在AC边上而在AC边的延长线上时,如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF.
【答案】(1)见解析;(2)(1)中的结论成立,证明见解析;(3)见解析.
【解析】
(1)欲证明AD=CE,只要证明△ABD≌△CBE即可.
(2)如图2中,倍长BE到H,连CH,DH.首先证明△DBH是等边三角形,由(1)可知,△ABD≌△CBH,推出AD=CH,∠A=∠HCB=∠ABC=60°,推出BF∥CH,推出∠F=∠ECH,再证明△EBF≌△EHC,推出BF=CH,由此即可证明.
(3)如图2中,倍长BE到H,连CH,DH.利用(1)中结论可得AD=CH,再证明BF=CH即可解决问题.
(1)证明:如图1中,
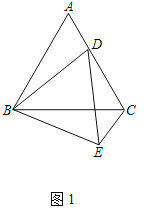
∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
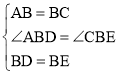 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE.
(2)如图2中,
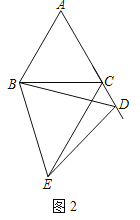
∵△ABC,△BDE都是等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
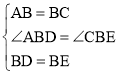 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE.
(3)如图2中,倍长BE到H,连CH,DH.
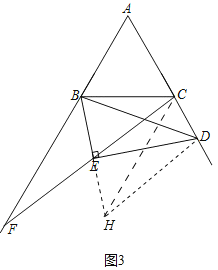
∵BE=EH,DE⊥BH,
∴DB=DH,∠BDE=∠HDE=30°,
∴∠BDH=60°,
∴△DBH是等边三角形,
由(1)可知,△ABD≌△CBH,
∴AD=CH,∠A=∠HCB=∠ABC=60°,
∴BF∥CH,
∴∠F=∠ECH,
在△EBF和△EHC中,
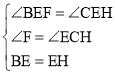 ,
,
∴△EBF≌△EHC(AAS),
∴BF=CH,
∴AD=BF.


科目:初中数学 来源: 题型:
【题目】我们已经学习了一元二次方程的解法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解方程.
(1)3(x-1)2=48;
(2)3x2-7x+4=0;
(3)x(2x+3)=4x+6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沅陵一中有360张旧棵桌需维修,经过甲、乙两个维修小组的竞标得知,甲组工作效率是乙组的1.5倍,且甲组单独维修完这批旧课桌比乙组单独维修完这批旧课桌少用5天;已知甲组每天需要付工资800元,乙组每天需要付工资400元;
(1)求甲、乙两个小组每天各维修多少张旧棵桌?
(2)学校维修这批旧课桌预算资金不超过7000元,时间不超过12天,请你帮学校算一算有几种维修方案(天数不足1天的按1天算);每种方案需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个不透明的布袋,甲布袋装有2个形状和重量完全相同的小球,分别标有数字1和2;乙布袋装有3个形状和重量完全相同的小球,分别标有数字﹣3,﹣1和0.先从甲布袋中随机取出一个小球,将小球上标有的数字记作x;再从乙布袋中随机取出一个小球,再将小球标有的数字记作y.
(1)用画树状图或列表法写出两次摸球的数字可能出现的所有结果;
(2)若从甲、乙两布袋中取出的小球上面的数记作点的坐标(x,y),求点(x,y)在一次函数y=﹣2x+1图象上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中有1个红球和2个黑球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录颜色后放回,搅匀,再从中任意摸出1个球,像这样有放回地先后摸球2次.摸出红球得2分,摸出黑球得1分.
(1)第一次摸出黑球的概率是多少?
(2)两次摸球所得总分为4分的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45![]() ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com