
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

【答案】(1)见解析;(2)见解析
【解析】
(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有∠CAD=∠BAD=45°,AD=BD=CD,而∠B=∠C=45°,所以∠B=∠DAF,再加上BE=AF,AD=BD,可证出:△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即△DEF是等腰直角三角形;
(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.
解:(1)连结AD ,
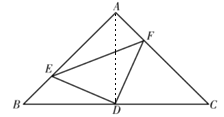
∵AB=AC ,∠BAC=90° ,D为BC中点 ,
∴AD⊥BC ,BD=AD ,
∴∠B=∠BAD=∠DAC=45°,
又∵BE=AF ,
∴△BDE≌△ADF(SAS),
∴ED=FD ,∠BDE=∠ADF,
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,
∴△DEF为等腰直角三角形.
(2)连结AD
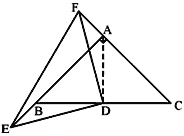
∵AB=AC ,∠BAC=90° ,D为BC中点 ,
∴AD=BD ,AD⊥BC ,
∴∠DAC=∠ABD=45° ,
∴∠DAF=∠DBE=135°,
又∵AF=BE ,
∴△DAF≌△DBE(SAS),
∴FD=ED ,∠FDA=∠EDB,
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF为等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD; (2)如果⊙O的半径为5,DE=1,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有A、B两种商品,已知在打折前,买60件A商品和30件B商品共用了1080元,买50件A商品和10件B商品共用了840元,A、B两种商品打相同折以后,某人买500件A商品和450件B商品一共花了7840元,请你计算A、B商品打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和等边△DBE,点D始终在射线AC上运动.
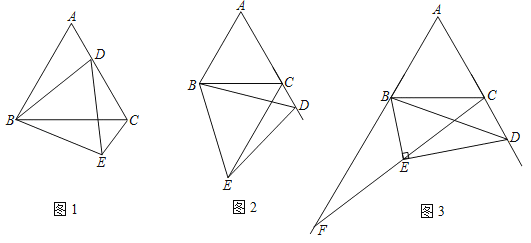
(1)如图1,当点D在AC边上时,连接CE,求证:AD=CE;
(2)如图2,当点D不在AC边上而在AC边的延长线上时,连接CE,(1)中的结论是否成立,并给予证明.
(3)如图3,当点D不在AC边上而在AC边的延长线上时,如果以BD为斜边作Rt△BDE,且∠BDE=30°,连接CE并延长,与AB的延长线交于F点,求证:AD=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,BD 是 AC 边上的高,延长 BC 到 E使 CE=CD,则图中等腰三角形的个数是()

A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com