
【题目】如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD; (2)如果⊙O的半径为5,DE=1,求AE的长.

【答案】(1)详见解析;(2)7.
【解析】
(1)欲证明AB=CD,只需证得![]() =
=![]() ;
;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
(1)证明:如图,∵AD=BC,
∴![]() =
=![]() ,
,
∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() ,即
,即![]() =
=![]() ,
,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
![]() ,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.


科目:初中数学 来源: 题型:
【题目】从﹣2,﹣1,0,1,2,3,4这7个数中任选一个数作为a的值,则使得关于x的分式方程![]() 有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
有整数解,且关于x的一次函数y=(a+1)x+a﹣4的图象不经过第二象限的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“建设社会主义新农村”工作组到某乡大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知:平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备,其费用p(万元)与大棚面积x(公顷)的函数关系式为p=0.9x2;另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.若某菜农期望通过种植大棚蔬菜当年获得5万元收益(扣除修建和种植成本后),从投入的角度考虑应建议他修建多少公项大棚?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习了一元二次方程的解法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解方程.
(1)3(x-1)2=48;
(2)3x2-7x+4=0;
(3)x(2x+3)=4x+6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知P是半径为5cm的⊙O内一点.解答下列问题:

(1)用尺规作图找出圆心O的位置.(要求:保留所有的作图痕迹,不写作法)
(2)用三角板分别画出过点P的最长弦AB和最短弦CD.
(3)已知OP=3cm,过点P的弦中,长度为整数的弦共有 _________ 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示为一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示.已知展开图中每个正方形的边长为1:
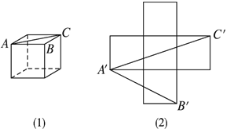
(1)在展开图(2)中可画出最长线段的长度为 ,在平面展开图(2)中这样的最长线段一共能画出 条。
(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com