
分析 本题应先求出OA的长,再分别讨论OA=OP、AP=OA、AP=OP的各种情况,即可得出答案.
解答 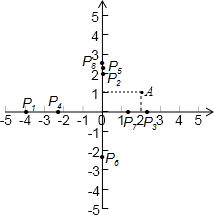 解:OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OA=OP时,x轴上有($\sqrt{5}$,0),(-$\sqrt{5}$,0);
解:OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OA=OP时,x轴上有($\sqrt{5}$,0),(-$\sqrt{5}$,0);
y轴上有(0,$\sqrt{5}$),(0,-$\sqrt{5}$);
AP=OA时,x轴上有(4,0),y轴上(0,2);
AP=OP时,x轴上有($\frac{5}{4}$,0)y轴上有(0,$\frac{5}{2}$)
∴所有存在的点P的坐标为:p1(4,0),p2(0,2),p3($\sqrt{5}$,0),p4(-$\sqrt{5}$,0),p5(0,$\sqrt{5}$),p6(0,-$\sqrt{5}$),p7($\frac{5}{4}$,0),p8(0,$\frac{5}{2}$),共8个,
故答案为:8.
点评 本题考查了坐标与图形的性质和等腰三角形的判定;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底,哪边是腰时,应在符合三角形三边关系的前提下分类讨论.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:选择题
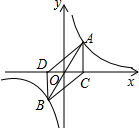 如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )
如图:A,B是函数y=$\frac{2}{x}$的图象上关于原点O点对称的任意两点,AC垂直于x轴于点C,BD垂直于y轴于点D,设四边形ADBC的面积为S,则( )| A. | S=2 | B. | 2<S<4 | C. | S=4 | D. | S>4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
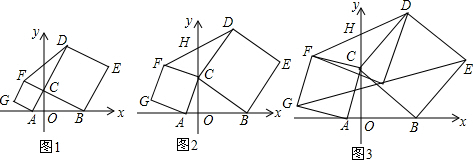
 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
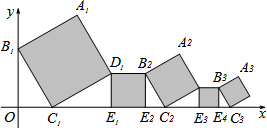 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )| A. | $\frac{1+\sqrt{3}}{9}$ | B. | $\frac{3+\sqrt{3}}{9}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | $\frac{1+\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com