
【题目】如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是 .①BE=CD;②∠BOD=60;③△BOD∽△COE.

【答案】①②
【解析】
∵△ABD与△AEC都是等边三角形,
∴AD=AB,AE=AC,∠ADB=∠ABD=60 ,∠DAB=∠EAC=60,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中

∴△DAC≌△BAE(SAS),
∴BE=DC,∠ADC=∠ABE,
∵∠BOD=180 ∠ODB∠DBA∠ABE=180 ∠ODB60 ∠ADC=120(∠ODB+∠ADC)=12060=60
∴∠BOD=60,
∴①正确;②正确;
∵△ABD与△AEC都是等边三角形,
∴∠ADB=∠AEC=60 ,但根据已知不能推出∠ADC=∠AEB,
∴说∠BDO=∠CEO错误,
∴△BOD∽△COE错误,
∴③错误;
故答案为:①②.


科目:初中数学 来源: 题型:
【题目】布袋中有红、黄、白三种乒乓球,个数依次为1个、2个、3个.除颜色外无其他差别,质感相同.
(1)小王随机地从袋中摸出1个乒乓球,摸出的是白色的概率是多少?
(2)小王随机地从袋中摸出两个乒乓球,求摸出的都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:(1)△ABP≌△AEQ;(2)EF=BF
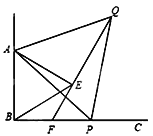
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地之间路程为4500米,甲、乙两人骑车都从A地出发,已如甲先出发6分钟后,乙才出发,乙在A、B之间的C地追赶上甲,当乙追赶上甲后,乙立即返A地,甲继续向B地前行.甲到达B地后停止骑行.乙骑行到A地时也停止(假定乙在C地掉头的时间忽略不计),在整个骑行过程中,甲和乙均保持各自的速度匀速骑行,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与B地相距的路程是______米.
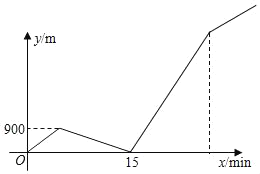
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() x2﹣
x2﹣![]() x﹣4交x轴于A、B两点,交y轴于点C.
x﹣4交x轴于A、B两点,交y轴于点C.
(1)点P为线段BC下方抛物线上的任意一点,一动点G从点P出发沿适当路径以每秒1个单位长度运动到y轴上一点M,再沿适当路径以每秒1个单位长度运动到x轴上的点N,再沿x轴以每秒![]() 个单位长度运动到点B.当四边形ACPB面积最大时,求运动时间t的最小值;
个单位长度运动到点B.当四边形ACPB面积最大时,求运动时间t的最小值;
(2)过点C作AC的垂线交x轴于点D,将△AOC绕点O旋转,旋转后点A、C的对应点分别为A1、C1,在旋转过程中直线A1C1与x轴交于点Q.与线段CD交于点I.当△DQI是等腰三角形时,直接写出DQ的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α等于( )

A. 20° B. 30° C. 40° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相交于点E,与AC相交于点F,AE平分∠BAC.

(1)求证:BC是⊙O的切线.
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.
(3)若AD=5,AE=4,求AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y=ax2+bx+c | … | t | m | ﹣2 | ﹣2 | n | … |
且当x=﹣![]() 时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<
时,与其对应的函数值y>0,有下列结论:①函数图象的顶点在第四象限内;②﹣2和3是关于x的方程ax2+bx+c=t的两个根;③0<m+n<![]() ,其中,正确结论的是( )
,其中,正确结论的是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数![]() 图象的两个交点.
图象的两个交点.

(1)求一次函数和反比例函数的解析式.
(2)求![]() 的面积.
的面积.
(3)观察图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com