
【题目】如图,在等边三角形![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的任意一点(不与点
上的任意一点(不与点![]() 重合),将
重合),将![]() 沿
沿![]() 折叠使点
折叠使点![]() 恰好落在等边三角形
恰好落在等边三角形![]() 的边上,则
的边上,则![]() 的长为_______cm.
的长为_______cm.
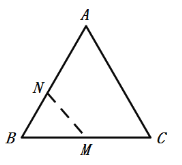
【答案】![]() 或
或![]()
【解析】
如图1,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边AB上时,于是得到MN⊥AB,BN=BN′,根据等边三角形的性质得到AC=BC,∠ABC=60°,根据线段中点的定义得到BN=![]() BM=
BM=![]() ,如图2,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A,C上时,则MN⊥BB′,四边形BMB′N是菱形,根据线段中点的定义即可得到结论.
,如图2,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A,C上时,则MN⊥BB′,四边形BMB′N是菱形,根据线段中点的定义即可得到结论.
解:如图1,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边AB上时,
则MN⊥AB,BN=BN′,
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°,
∵点M为边BC的中点,
∴BM=![]() BC=
BC=![]() AB=
AB=![]() ,
,
∴BN=![]() BM=
BM=![]() ,
,
如图2,当点B关于直线MN的对称点B'恰好落在等边三角形ABC的边A,C上时,
则MN⊥BB′,四边形BMB′N是菱形,
∵∠ABC=60°,点M为边BC的中点,
∴BN=BM=![]() BC=
BC=![]() AB=
AB=![]() ,,
,,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五关,分别用![]() 表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
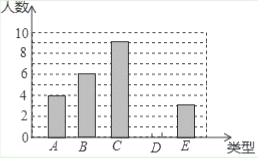
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、中位数;
(3)估计该单位750名职工共捐书多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:在现今“互联网+”的时代,密码与我们的生活已经紧密相连,密不可分,而诸如“123456”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了。有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:![]() 因式分解的结果为
因式分解的结果为![]() ,当
,当![]() 时,
时,![]() ,此时可以得到数字密码171920.
,此时可以得到数字密码171920.
(1)根据上述方法,当![]() 时,对于多项式
时,对于多项式![]() 分解因式后可以形成哪些数字密码?(写出三个).
分解因式后可以形成哪些数字密码?(写出三个).
(2)若一个直角三角形的周长是24,斜边长为10,其中两条直角边分别为![]() ,求出一个由多项式
,求出一个由多项式![]() 分解因式后得到的密码(只需一个即可).
分解因式后得到的密码(只需一个即可).
(3)若多项式![]() 因式分解后,利用本题的方法,当
因式分解后,利用本题的方法,当![]() 时可以得到其中一个密码为2434,求
时可以得到其中一个密码为2434,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.

查看答案和解析>>
科目:初中数学 来源: 题型:
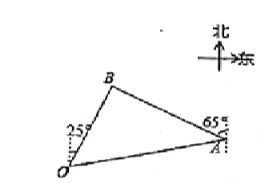
【题目】中国海军亚丁湾护航十年,中国海军被亚丁湾上来往的各国商船誉为“值得信赖的保护伞”.如图,在一次护航行动中,我国海军监测到一批可疑快艇正快速向护航的船队靠近,为保证船队安全,我国海军迅速派出甲、乙两架直升机分别从相距40海里的船队首(![]() 点)尾(
点)尾(![]() 点)前去拦截,8分钟后同时到达
点)前去拦截,8分钟后同时到达![]() 点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东
点将可疑快艇驱离.己知甲直升机每小时飞行180海里,航向为北偏东![]() ,乙直升机的航向为北偏西
,乙直升机的航向为北偏西![]() ,求乙直升机的飞行速度(单位:海里/小时).
,求乙直升机的飞行速度(单位:海里/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com