
(10分)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)判断OE与OF的大小关系?并说明理由;(4分)
(2)当点O运动到何处时,四边形AECF是矩形?并说出你的理由;(4分)
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AECF会是正方形.
不要写理由.(2分)
(1)OE=OF,理由详见解析;(2)当点O运动到AC的中点处,理由详见解析;(3)∠ACB=90°时.
【解析】
试题分析:(1)利用角平分线的性质得出,∠1=∠2,进而得出,∠3=∠2,即可得出OE与OF的大小关系;
(2)首先证得四边形AECF是平行四边形,进而得出∠ECF=90°,再利用矩形的判定得出即可;
(3)由(2)证明可知,当点O运动到AC的中点时,四边形AECF是矩形,进而得出AC⊥MN,即可得出答案.
试题解析:(1)OE=OF,理由如下:
因为CE平分∠ACB,所以∠1=∠2,又因为MN∥BC,所以∠1=∠3,所以∠3=∠2,所以EO=CO,同理,FO=CO,所以OE=OF.

(2)当点O运动到AC的中点时,四边形AECF是矩形,理由如下:
因为OE=OF,点O是AC的中点,所以四边形AECF是平行四边形,又因为CF平分∠BCA的外角,所以∠4=∠5,又因为∠1=∠2,所以∠1=∠2,∠2+∠4=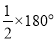 =90°,即∠ECF=90°,所以平行四边形AECF是矩形.
=90°,即∠ECF=90°,所以平行四边形AECF是矩形.
(3)当△ABC是直角三角形时,即∠ACB=90°时,四边形AECF是正方形,理由如下:
由(2)证明可知,当点O运动到AC的中点时,四边形AECF是矩形,又因为∠ACB=90°,CE,CN分别是∠ACB与∠ACB的外角的平分线,所以∠1=∠2=∠3=∠4=∠5=45°,所以AC⊥MN,所以四边形AECF是正方形.
考点:矩形的判定;平行四边形的判定;正方形的判定.


科目:初中数学 来源: 题型:
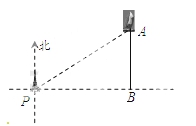
如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2 海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )
(A)2 海里 (B)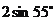 海里
海里
(C)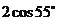 海里 (D)
海里 (D) 海里
海里
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市八年级下学期第一次月考数学试卷(解析版) 题型:选择题
等式4(x-2)>2(3x+5)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台第一教研片七年级下学期第一次月考数学卷(解析版) 题型:选择题
下列计算正确的是( ).
A.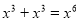 B.
B.
C. D.(2xy)3=2x3y
D.(2xy)3=2x3y
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台第一教研片八年级下学期第一次月考数学卷(解析版) 题型:填空题
我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.则矩形的中点四边形的是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省衡阳市七年级上学期期末考试数学试卷(解析版) 题型:解答题
若2x| 2a+1 |y与 xy| b |是同类项,其中a、b互为倒数,求2(a-2b2)-
xy| b |是同类项,其中a、b互为倒数,求2(a-2b2)-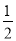 (3b2-a)的值.
(3b2-a)的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省衡阳市八年级上学期期末考试数学试卷(解析版) 题型:选择题
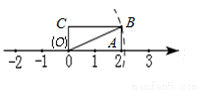
如图,矩形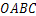 的边
的边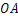 长为2,
长为2, 长为1,
长为1,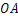 在数轴上,以原点
在数轴上,以原点 为圆心,对角线
为圆心,对角线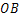 的长为半径画弧,交正半轴于一点,则这个点表示的实数是
的长为半径画弧,交正半轴于一点,则这个点表示的实数是
A.2.5 B.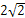 C.
C.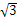 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com