
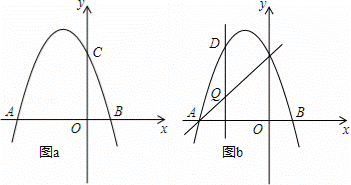
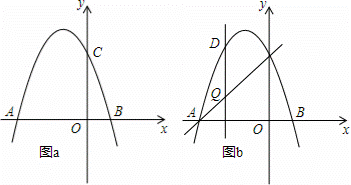
如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
解:(1)把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
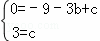 ,
,
解得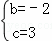 .
.
故该抛物线的解析式为:y=﹣x2﹣2x+3.
(2)由(1)知,该抛物线的解析式为y=﹣x2﹣2x+3,则易得B(1,0).
∵S△AOP=4S△BOC,
∴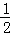 ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4×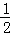 ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±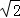 .
.
则符合条件的点P的坐标为:(﹣1,4)或(﹣1+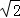 ,﹣4)或(﹣1﹣
,﹣4)或(﹣1﹣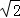 ,﹣4);
,﹣4);
(3)设直线AC的解析式为y=kx+t,将A(﹣3,0),C(0,3)代入,
得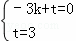 ,
,
解得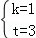 .
.
即直线AC的解析式为y=x+3.
设Q点坐标为(x,x+3),(﹣3≤x≤0),则D点坐标为(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+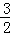 )2+
)2+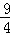 ,
,
∴当x=﹣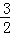 时,QD有最大值
时,QD有最大值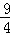 .
.


科目:初中数学 来源: 题型:
已知三条不同的直线a、b、c在同一平面内,下列四条命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是S甲2=0.35,S乙2=0.15,S丙2=0.25,S丁2=0.27,这4人中成绩发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
李华根据演讲比赛中九位评委所给的分数制作了如下表格:
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
如果要去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数 B. 众数 C. 方差 D.中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图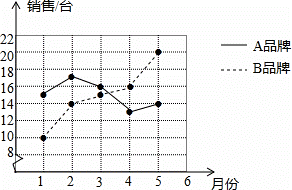
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根 据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com