
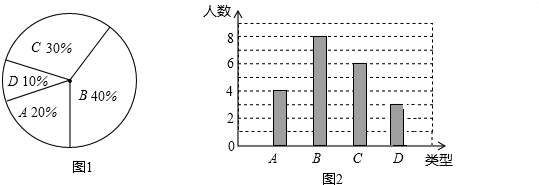

���� ��1������ͳ��ͼ��D����������ӦΪ20��10%��
��2����������ͳ��ͼ������ͳ��ͼ�ó���������λ�����ɣ�
��3����С��ķ����Ǵӵڶ�����ʼ���ִ���ģ�
�������ȷ��ƽ����������380���ɵõ������
��� �⣺��1������ͳ��ͼ��D����Ϊ3�˴��ˣ�Ӧ����
20��10%=2���ˣ���
��2��20��ѧ��ÿ��ֲ������������5�ã���λ����5�ã�
��3���ٵڶ�����
����ȷ��ƽ�����ǣ�
$\overline{x}$=$\frac{4��4+5��8+6��6+7��2}{20}$=5.3���ã�
������380��ѧ����ֲ��380��5.3=2014���ã���
���� ���⿼��������ͳ��ͼ������ͳ��ͼ����Ȩƽ�������Լ��������������壬Ū�������ͳ��ͼ���ҳ������Լ����㷽���ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5a+a=5a2 | B�� | 5a+b=5ab | C�� | 5a2b-3ab2=2a2b | D�� | 2ab2-5b2a=-3ab2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=1��y=2 | B�� | x=2��y=-1 | C�� | x=0��y=2 | D�� | x=3��y=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1��ƽ��ֱ������ϵ�У�ֱ��l1��y�ύ�ڵ�A����B��-3��3��Ҳ��ֱ��l1�ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����Cǡ��Ҳ��ֱ��l1�ϣ�
��ͼ��ֱ��l1��ƽ��ֱ������ϵ�У�ֱ��l1��y�ύ�ڵ�A����B��-3��3��Ҳ��ֱ��l1�ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����Cǡ��Ҳ��ֱ��l1�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A�Ƿ���������y=$\frac{2}{x}$��x��0����ͼ��������һ�㣬AB��x�ύ����������y=-$\frac{3}{x}$��ͼ���ڵ�B����ABΪ������ABCD������C��D��x���ϣ���S��ABCDΪ��������
��ͼ����A�Ƿ���������y=$\frac{2}{x}$��x��0����ͼ��������һ�㣬AB��x�ύ����������y=-$\frac{3}{x}$��ͼ���ڵ�B����ABΪ������ABCD������C��D��x���ϣ���S��ABCDΪ��������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����AC=2��BC=2$\sqrt{3}$����ͼ����Ӱ���ֵ����Ϊ$\frac{4��}{3}$-$\sqrt{3}$��
��ͼ��AB�ǡ�O��ֱ����AC=2��BC=2$\sqrt{3}$����ͼ����Ӱ���ֵ����Ϊ$\frac{4��}{3}$-$\sqrt{3}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com