
【题目】已知点P(![]() ,
,![]() )和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
【答案】(1)![]() ;(2)见解析;(3)2
;(2)见解析;(3)2![]() .
.
【解析】
(1)根据点P到直线y=kx+b的距离公式直接计算即可;(2)先利用点到直线的距离公式计算出圆心Q到直线y=![]() x+9,然后根据切线的判定方法可判断⊙Q与直线y=
x+9,然后根据切线的判定方法可判断⊙Q与直线y=![]() x+9相切;(3)利用两平行线间的距离定义,在直线y=-2x+4上任意取一点,然后计算这个点到直线y=-2x-6的距离即可.
x+9相切;(3)利用两平行线间的距离定义,在直线y=-2x+4上任意取一点,然后计算这个点到直线y=-2x-6的距离即可.
(1)因为直线y=x-1,其中k=1,b=-1,
所以点P(1,-1)到直线y=x-1的距离为:d=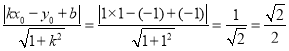 ;
;
(2)⊙Q与直线y=![]() x+9的位置关系为相切.
x+9的位置关系为相切.
理由如下:
圆心Q(0,5)到直线y=![]() x+9的距离为:d=
x+9的距离为:d=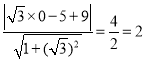 ,
,
而⊙O的半径r为2,即d=r,
所以⊙Q与直线y=![]() x+9相切;
x+9相切;
(3)当x=0时,y=-2x+4=4,即点(0,4)在直线y=-2x+4,
因为点(0,4)到直线y=-2x-6的距离为:d=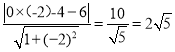 ,
,
因为直线y=-2x+4与y=-2x-6平行,
所以这两条直线之间的距离为2![]() .
.


科目:初中数学 来源: 题型:
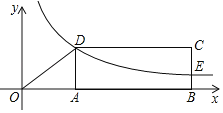
【题目】如图,矩形ABCD的顶点A、B在x轴的正半轴上,反比例函数y=![]() (k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=
(k≠0)在第一象限内的图象经过点D,交BC于点E.若AB=4,CE=2BE,tan∠AOD=![]() ,则k的值_____.
,则k的值_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+ax+3的顶点为P,它分别与x轴的负半轴、正半轴交于点A,B,与y轴正半轴交于点C,连接AC,BC,若tan∠OCB﹣tan∠OCA=![]() .
.
(1)求a的值;
(2)若过点P的直线l把四边形ABPC分为两部分,它们的面积比为1:2,求该直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数 的图象与性质.列表:
的图象与性质.列表:

描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.

![]() 如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
![]() 研究函数并结合图象与表格,回答下列问题:
研究函数并结合图象与表格,回答下列问题:
![]() 点
点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,则
在函数图象上,则![]() ______
______![]() ,
,![]() ______
______![]() ;
;![]() 填“
填“![]() ”,“
”,“![]() ”或“
”或“![]() ”
”![]()
![]() 当函数值
当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
![]() 在直线
在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
![]() 若直线
若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数![]() 图象与x轴交于点A,与y轴交于点B.
图象与x轴交于点A,与y轴交于点B.
(1)请直接写出点A坐标______,点B坐标________;
(2)点C是直线AB上一个动点,当△AOC的面积是△BOC的面积的2倍时,求点C的坐标;
(3)点D为直线AB上的一个动点,在平面内找另一个点E,且以O、B、D、E为顶点的四边形是菱形,请直接写出满足条件的菱形的周长_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有三张卡片,每张卡片上写有1个实数,分别为1,2,3.(卡片除了实数不同外,其余均相同)
(1)从盒子中随机抽取一张卡片,请直接写出卡片上的实数是2的概率_______;
(2)先从盒子中随机抽取一张卡片,将卡片上的实数作为点P的横坐标,卡片不放回,再随机抽取一张卡片,将卡片上的实数作为点P的纵坐标,两次抽取的卡片上的实数分别作为点P的横纵坐标.请你用列表法或树状图法,求出点P在反比例函数![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调查价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.
(1)直接写出每周售出商品的利润y(单位:元)与每件降价x(单位:元)之间的函数关系式,直接写出自变量x的取值范围;
(2)涨价多少元时,每周售出商品的利润为2250元;
(3)直接写出使每周售出商品利润最大的商品的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
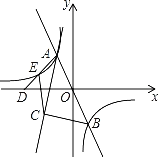
【题目】如图,过原点的直线y1=mx(m≠0)与反比例函数y2=![]() (k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为
(k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为![]() .
.
(1)根据图象回答:当x取何值时,y1<y2;
(2)求△AOD的面积;
(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com