
【题目】某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调查价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.
(1)直接写出每周售出商品的利润y(单位:元)与每件降价x(单位:元)之间的函数关系式,直接写出自变量x的取值范围;
(2)涨价多少元时,每周售出商品的利润为2250元;
(3)直接写出使每周售出商品利润最大的商品的售价.
【答案】(1)y=﹣20x2+100x+6000;(0≤x≤20);(2)涨价25元时,每周售出商品的利润为2250元;(3)65元.
【解析】
(1)根据涨价时,每涨价1元,每星期要少卖出10件,可列出销售量的代数式,根据总利润=单件利润×销售量列出函数表达式即可;
(2)根据总利润=单件利润×销售量列方程解答即可;
(3)根据函数表达式,利用二次函数的性质解答即可.
解:(1)∵每降价1元,每星期要多卖出20件,
∴每星期实际可卖出(300+20x)件,
y=(60﹣40﹣x)(300+20x)
=﹣20x2+100x+6000;(0≤x≤20);
(2)设涨价m元时,每周售出商品的利润为2250元,
由题意得,(60+m﹣40)(300﹣10m)=2250,
解得:m=25或m=﹣15(不合题意,舍去);
答:涨价25元时,每周售出商品的利润为2250元;
(3)∵y=-20x2+100x+6000=-20(x-![]() )2+6125.
)2+6125.
∴在降价的情况下,售价为57.5元每星期售出商品的最大利润是6125元.
设涨价m元时,每周售出商品的利润为W元,
∴W=(60+m-40)(300-10m)=-10m2+100m+6000=-10(m-5)2+6250,
∴在涨价的情况下,售价为65元每星期售出商品的最大利润是6250元.
综上所述:每周售出商品利润最大的商品的售价是65元.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
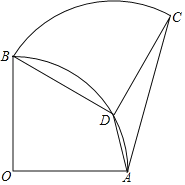
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(![]() ,
,![]() )和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机抽取部分学生就“你是否喜欢网课”进行问卷调查,并将调查结果进行统计后,绘制成如下统计表和扇形统计图.
调查结果统计表

(1)在统计表中,a= ,b= ;
(2)求出扇形统计图中“喜欢”网课所对应扇形的圆心角度数;
(3)已知该校共有2000名学生,试估计该校“非常喜欢”网课的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
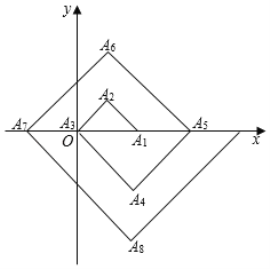
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
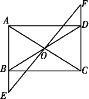
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
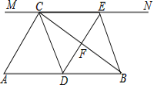
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:DF=![]() AC
AC
(2)试判断四边形BECD是什么特殊四边形?说明你的理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司展销如图所示的长方形工艺品,该工艺品长60![]() ,宽40
,宽40![]() ,中间镶有宽度相同的三条丝绸花边.
,中间镶有宽度相同的三条丝绸花边.

(1)若丝绸花边的面积(阴影面积)为650![]() ,求丝绸花边的宽度;
,求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
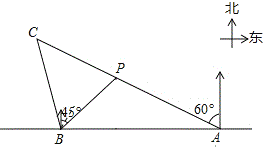
【题目】2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(12+4![]() )海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
)海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
(1)求B、P两点之间的距离;(结果有根号的保留根号)
(2)山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15°的方向.在这次训练中,山东舰的航行速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com