
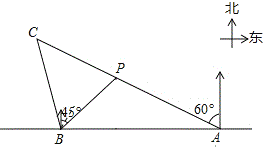
【题目】2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(12+4![]() )海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
)海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
(1)求B、P两点之间的距离;(结果有根号的保留根号)
(2)山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15°的方向.在这次训练中,山东舰的航行速度是多少?
【答案】(1)4![]() 海里;(2)航行速度为24海里/时
海里;(2)航行速度为24海里/时
【解析】
(1)过P作PH⊥AB,垂足为H,设PH=x,利用解直角三角形求出PH的长度,然后即可求出BP的长度;
(2)过P作PM⊥BC于M,由解直角三角形求出PC的长度,然后即可求出速度.
解:(1)过P作PH⊥AB,垂足为H,设PH=x,
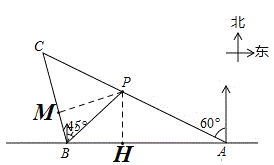
在Rt△BPH中,∠PBH=45°,
则BH=x,PB=![]() ;
;
在Rt△APH中,∠PAB=30°,![]() =tan30°,
=tan30°,
则AH=![]() x;
x;
∴AB=x+![]() x=12+4
x=12+4![]() ,
,
解得:x=4![]() ,
,
∴BP=![]() =4
=4![]() (海里).
(海里).
(2)过P作PM⊥BC于M,
在Rt△BPM中,∠PBC=60°,则BM=2![]() ,PM=
,PM=![]() ;
;
在Rt△PMC中,∠CPM=45°,![]() =cos45°,则PC=12.
=cos45°,则PC=12.
航行速度为12÷0.5=24(海里/时).
答:BP=4![]() 海里,航行速度为24海里/时.
海里,航行速度为24海里/时.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调查价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.
(1)直接写出每周售出商品的利润y(单位:元)与每件降价x(单位:元)之间的函数关系式,直接写出自变量x的取值范围;
(2)涨价多少元时,每周售出商品的利润为2250元;
(3)直接写出使每周售出商品利润最大的商品的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
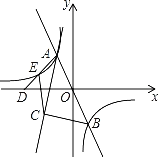
【题目】如图,过原点的直线y1=mx(m≠0)与反比例函数y2=![]() (k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为
(k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为![]() .
.
(1)根据图象回答:当x取何值时,y1<y2;
(2)求△AOD的面积;
(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
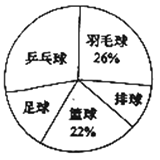
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(![]() ,
,![]() );
);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是________.
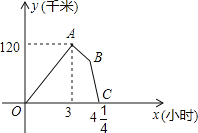
A.①②③④B.①③④C.①③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是________.
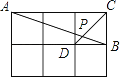
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距150km,甲、乙两人先后从A地出发向B地行驶,甲骑摩托车匀速行驶,乙开汽车且途中速度只改变一次,如图表示的是甲、乙两人之间的距离S关于时间t的函数图象(点F的实际意义是乙开汽车到达B地),请根据图象解答下列问题:
(1)求出甲的速度;
(2)求出乙前后两次的速度,并求出点E的坐标;
(3)当甲、乙两人相距10km时,求t的值.
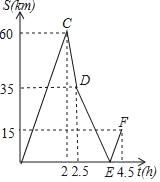
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D在⊙O上两点,连接AD,CD.
(1)如图1,点P是AC延长线上一点,∠APB=∠ADC,求证:BP与⊙O相切;
(2)如图2,点G在CD上,OF⊥AC于点F,连接AG并延长交⊙O于点H,若CD为⊙O的直径,当∠CGB=∠HGB,BG=2OF=6时,求⊙O半径的长.
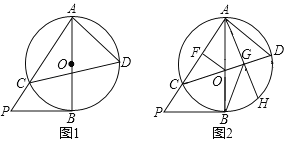
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨![]() ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com