
【题目】如图,过原点的直线y1=mx(m≠0)与反比例函数y2=![]() (k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为
(k<0)的图象交于A、B两点,点A在第二象限,且点A的横坐标为﹣1,点D在x轴负半轴上,连接AD交反比例函数图象于另一点E,AC为∠BAD的平分线,过点B作AC的垂线,垂足为C,连接CE,若AD=2DE,△AEC的面积为![]() .
.
(1)根据图象回答:当x取何值时,y1<y2;
(2)求△AOD的面积;
(3)若点P的坐标为(m,k),在y轴的轴上是否存在一点M,使得△OMP是直角三角形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
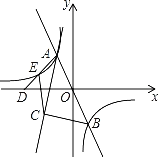
【答案】(1)﹣1<x<0或x>1;(2)3;(3)存在,点M的坐标为(0.﹣2)或(0,﹣4).
【解析】
(1)根据题意得到点A,点B关于原点对称,求得点B的横坐标为1,于是得到当x取﹣1<x<0或x>1时,y1<y2;
(2)连接OC,OE,求得OA=OB,得到∠OAC=∠OCA,根据角平分线的定义得到∠OAC=∠DAC,推出AD//OC,得到![]() ,即可得到答案;
,即可得到答案;
(3)作EF⊥x轴于F,AH⊥x轴于H,则EF//AH,求得DF=FH,根据三角形中位线定理得到EF=![]() AH,求得y=﹣
AH,求得y=﹣![]() ,得到A(﹣1,2),于是得到P(﹣2,﹣2),根据直角三角形的性质即可得到结论.
,得到A(﹣1,2),于是得到P(﹣2,﹣2),根据直角三角形的性质即可得到结论.
解:(1)∵直线![]() =mx(m≠0)与反比例函数
=mx(m≠0)与反比例函数![]() (k<0)的图象交于A、B两点,且点A的横坐标为﹣1,
(k<0)的图象交于A、B两点,且点A的横坐标为﹣1,
∴点A,点B关于原点对称,
∴点B的横坐标为1,
∴当x取﹣1<x<0或x>1时,y1<y2;
(2)连接OC,OE,
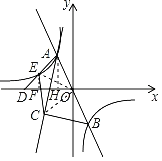
由图象知,点A,点B关于原点对称,
∴OA=OB,
∵AC⊥CB,
∴∠ACB=90°,
∴OC=![]() AB=AO,
AB=AO,
∴∠OAC=∠OCA,
∵AC为∠BAD的平分线,
∴∠OAC=∠DAC,
∴∠OCA=∠DAC,
∴AD//OC,
∴![]() ,
,
∵AD=2DE,
∴AE=DE,
∴![]() ;
;
(3)作EF⊥x轴于F,作AH⊥x轴于H,如上图,
则EF//AH,
∵AD=2DE,
∴DE=EA,
∵EF//AH,
∴![]() ,
,
∴DF=FH,
∴EF是△DHA的中位线,
∴EF=![]() AH,
AH,
∵![]()
∴OFEF=OHHA,
∴OH=![]() OF,
OF,
∴OH=HF,
∴DF=FH=HO=![]() DO,
DO,
∴![]() ,
,
∴![]() ,
,
∴k=﹣2,
∴y=![]() ,
,
∵点A在y=![]() 的图象上,
的图象上,
∴把x=﹣1代入得,y=2,
∴A(﹣1,2),
∵点A在直线y=mx上,
∴m=﹣2,
∴P(﹣2,﹣2),
在y轴上找到一点M,使得△OMP是直角三角形,
当∠OMP=90°时,PM⊥y轴,
则OM=2,
∴点M的坐标为(0.﹣2);
当∠OPM=90°时,过P作PG⊥y轴于G,则△OPM是等腰直角三角形,
∴OM=2PG=4,
∴点M的坐标为(0.﹣4);
综上所述,点M的坐标为(0.﹣2)或(0,﹣4).


科目:初中数学 来源: 题型:
【题目】已知点P(![]() ,
,![]() )和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=![]() =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
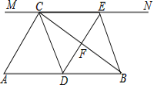
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上中点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:DF=![]() AC
AC
(2)试判断四边形BECD是什么特殊四边形?说明你的理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司展销如图所示的长方形工艺品,该工艺品长60![]() ,宽40
,宽40![]() ,中间镶有宽度相同的三条丝绸花边.
,中间镶有宽度相同的三条丝绸花边.

(1)若丝绸花边的面积(阴影面积)为650![]() ,求丝绸花边的宽度;
,求丝绸花边的宽度;
(2)已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大,最大利润是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝防控新冠肺炎疫情的胜利,某校举行班级抗击疫情优秀歌曲歌咏比赛,歌曲有:《逆行英雄》,《中国一定强》,《爱的承诺》(分别用字母A,B,C,依次表示这三首歌曲),比赛时,将A,B,C,这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,九年一班班长先从中随机抽取一张卡片,放回后洗匀,再由九年二班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)九年一班抽中歌曲《中国一定强》的概率是 ;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出九年一班和九年二班抽中相同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,某国遭遇了近年来最大的经济危机,导致该国股市大幅震荡,昨天某支股票累计卖出的数量和交易时间之间的关系如图中虚线所示,累计买入的数量和交易时间之间的关系如图中实线所示,其中点A是实线和虚线的交点,点C是BE的中点,CD与横轴平行,则下列关于昨天该股票描述正确的是( )
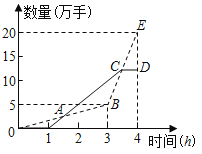
A.交易时间在3.5h时累计卖出的数量为12万手
B.交易时间在1.4h时累计卖出和累计买入的数量相等
C.累计卖出的数量和累计买入的数量相差1万手的时刻有5个
D.从点A对应的时刻到点C对应的时刻,平均每小时累计卖出的数量小于买入的数量
查看答案和解析>>
科目:初中数学 来源: 题型:
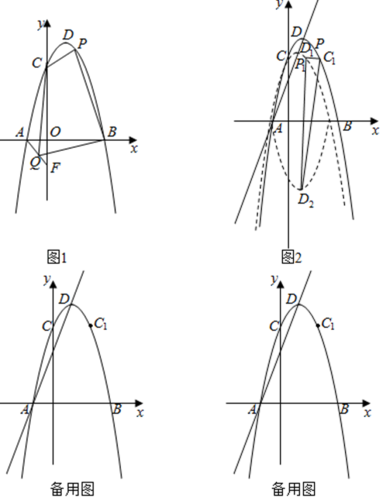
【题目】在平面直角坐标系中,抛物线y=﹣ax2+2ax+c与x轴相交于A(﹣1,0)、B两点(A点在B点左侧),与y轴相交于点C(0,3![]() ),点D是抛物线的顶点.
),点D是抛物线的顶点.
(1)如图1,求抛物线的解析式;
(2)如图1,点F(0,b)在y轴上,连接AF,点Q是线段AF上的一个动点,P是第一象限抛物线上的一个动点,当b=﹣![]() 时,求四边形CQBP面积的最大值与点P的坐标;
时,求四边形CQBP面积的最大值与点P的坐标;
(3)如图2,点C1与点C关于抛物线对称轴对称.将抛物线y沿直线AD平移,平移后的抛物线记为y1,y1的顶点为D1,将抛物线y1沿x轴翻折,翻折后的抛物线记为y2,y2的顶点为D2.在(2)的条件下,点P平移后的对应点为P1,在平移过程中,是否存在以P1D2为腰的等腰△C1P1D2,若存在请直接写出点D2的横坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
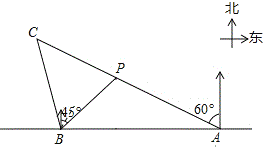
【题目】2019年12月17日,国产航母山东舰正式交付中国海军,中国海军建设迈上了一个新台阶.如图,在一次训练中,笔直的海岸线l上有A、B两个观测站,A在B的正东方向,AB=(12+4![]() )海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
)海里,山东舰在点P处,从A测得山东舰在北偏西60°的方向,从B测得山东舰在北偏东45°的方向.
(1)求B、P两点之间的距离;(结果有根号的保留根号)
(2)山东舰从点P处沿射线AP的方向航行,航行30分钟后到达点C处,此时,从B测得山东舰在北偏西15°的方向.在这次训练中,山东舰的航行速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com