
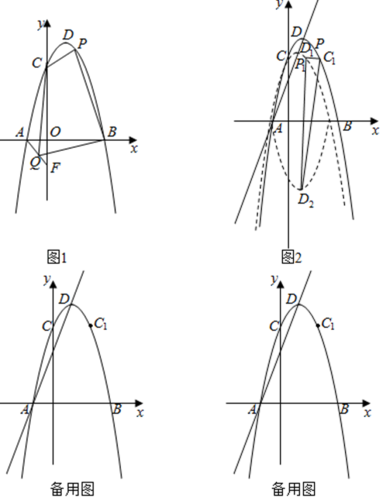
����Ŀ����ƽ��ֱ������ϵ�У�������y����ax2+2ax+c��x���ཻ��A����1��0����B���㣨A����B����ࣩ����y���ཻ�ڵ�C��0��3![]() ������D�������ߵĶ��㣮
������D�������ߵĶ��㣮
��1����ͼ1���������ߵĽ���ʽ��
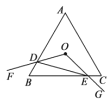
��2����ͼ1����F��0��b����y���ϣ�����AF����Q���߶�AF�ϵ�һ�����㣬P�ǵ�һ�����������ϵ�һ�����㣬��b����![]() ʱ�����ı���CQBP��������ֵ���P�����ꣻ
ʱ�����ı���CQBP��������ֵ���P�����ꣻ
��3����ͼ2����C1���C���������߶Գ���Գƣ���������y��ֱ��ADƽ�ƣ�ƽ�ƺ��������Ϊy1��y1�Ķ���ΪD1����������y1��x�ᷭ�ۣ����ۺ��������Ϊy2��y2�Ķ���ΪD2���ڣ�2���������£���Pƽ�ƺ�Ķ�Ӧ��ΪP1����ƽ�ƹ����У��Ƿ������P1D2Ϊ���ĵ�����C1P1D2����������ֱ��д����D2�ĺ����꣬����������˵�����ɣ�
���𰸡���1��y����![]() x2+2
x2+2![]() x+3
x+3![]() ����2����m��
����2����m��![]() ʱ��S�ı���CQBPȡ�����ֵ
ʱ��S�ı���CQBPȡ�����ֵ![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
��![]() ������3�����ڣ�����Ҫ���D2�ĺ������У�
������3�����ڣ�����Ҫ���D2�ĺ������У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
��1����A��C����������������߽���ʽ�������a��c��ֵ���ɣ�
��2�������B��F���꣬Ȼ�����֤��AF��BCƽ�У����ǡ�QBC������͵��ڡ�ABC������������ת��Ϊ���PBC����������ֵ����PE��y�ύֱ��BC��E����P��ĺ�����Ϊδ֪��m����E������Ҳ��m��ʾ��PE�ij�����P��E������֮���ʾ�����ǡ�PBC������Ϳ��Ա�ʾ�ɹ���m�Ķ��κ�����ͨ���䷽�����������ֵ��P�����꣮
��3������������P1D2Ϊ������˷�������ֱ��з��̼��㼴�ɣ�
��1����A����1��0����C��0��3![]() �����������߽���ʽ�ã�
�����������߽���ʽ�ã�
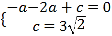
��ã� ��
��
�������ߵĽ���ʽΪy����![]() x2+2
x2+2![]() x+3
x+3![]() ��
��
��2����ͼ1������BC��AC����PE��y�ύBC��E��
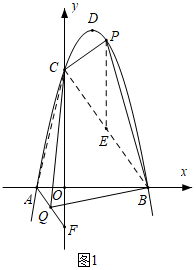
��y����![]() x2+2
x2+2![]() x+3
x+3![]() ����
����![]() ��x+1����x��3����
��x+1����x��3����
��B��3��0����
��b����![]() ��
��
��F��0����![]() ����
����
��![]() ��
��![]() ��
��
��AF��BC��
��S��QBC��S��ABC��![]() ABOC��6
ABOC��6![]() ��
��
��B��C��������ɵ�ֱ��BC�Ľ���ʽΪ��y����![]() x+3
x+3![]() ��
��
��P��m����![]() m2+2
m2+2![]() m+3
m+3![]() ������E��m����
������E��m����![]() m+3
m+3![]() ����
����
PE��yP��yE����![]() m2+4
m2+4![]() m��
m��
��S��PBC��![]() ��xB��xC����yP��yE������
��xB��xC����yP��yE������![]() m2+6
m2+6![]() m����
m����![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
��S�ı���CQBP��S��QBC+S��PBC��S��ABC+S��PBC����![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
�൱m��![]() ʱ��S�ı���CQBPȡ�����ֵ
ʱ��S�ı���CQBPȡ�����ֵ![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
��![]() ����
����
��3����y����![]() x2+2
x2+2![]() x+3
x+3![]() ��
��![]() ��
��
��D��1��4![]() ���������߶Գ���Ϊx��1��
���������߶Գ���Ϊx��1��
��C1��C����ֱ��x��1�Գƣ�
��C1��2��3![]() ����
����
��A��D������������ֱ��AD�Ľ���ʽΪy��2![]() x+2
x+2![]() ��
��
��D1��m��2![]() m+2
m+2![]() ����
����
��P1��m+![]() ��2
��2![]() m+
m+![]() ����D2��m����2
����D2��m����2![]() m��2
m��2![]() ����
����
��![]() ��
��![]() ��
��
![]() ��
��
��P1C1��P1D2ʱ��![]() ��
��![]() �����
�����![]() ��
��![]() ��
��
��C1D2��P1D2ʱ��9m2+36m+54��![]() �����
�����![]() ��
��![]() ��
��
��������������Ҫ���D2�ĺ������У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���ܳ�Ϊ36 cm���Խ���
���ܳ�Ϊ36 cm���Խ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() cm������
cm������![]() ��
��![]() ���е㣬��
���е㣬��![]() ���ܳ�Ϊ�� ��
���ܳ�Ϊ�� ��

A.10 cmB.15 cmC.20 cmD.30 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() .������
.������![]() ��һԪ���η���
��һԪ���η���![]() ��
��![]() �ķ�Χ����ʵ��������
�ķ�Χ����ʵ��������![]() ��ȡֵ��Χ��_____________.
��ȡֵ��Χ��_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
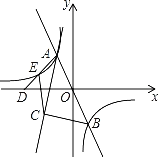
����Ŀ����ͼ����ԭ���ֱ��y1��mx��m��0���뷴��������y2��![]() ��k��0����ͼ����A��B���㣬��A�ڵڶ����ޣ��ҵ�A�ĺ�����Ϊ��1����D��x�Ḻ�����ϣ�����AD������������ͼ������һ��E��ACΪ��BAD��ƽ���ߣ�����B��AC�Ĵ��ߣ�����ΪC������CE����AD��2DE����AEC�����Ϊ
��k��0����ͼ����A��B���㣬��A�ڵڶ����ޣ��ҵ�A�ĺ�����Ϊ��1����D��x�Ḻ�����ϣ�����AD������������ͼ������һ��E��ACΪ��BAD��ƽ���ߣ�����B��AC�Ĵ��ߣ�����ΪC������CE����AD��2DE����AEC�����Ϊ![]() ��
��
��1������ͼ��ش𣺵�xȡ��ֵʱ��y1��y2��
��2�����AOD�������
��3������P������Ϊ��m��k������y��������Ƿ����һ��M��ʹ�á�OMP��ֱ�������Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
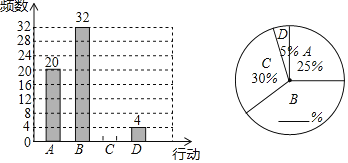
����Ŀ����������ˮƽ��������ߣ�����Խ��Խϲ�����ڣ����յ���ʽ���ս�Ũ�ң�ijУ�����ˡ�ĸ��ů���ر��ж�����������������˲���ͬѧ��ů���ж����������ΪA��B��C��D�������ͣ��ֱ��Ӧ�ͷ������ʻ����ͺ�����ͻ�����ָ��ݵ�������ݻ��Ƴ����µ�����ͳ��ͼ������ͳ��ͼ��
��������ϲ�������ͳ��ͼ�ṩ����Ϣ������������⣺
��1����У������˶�����ͬѧ��ů���ж���
��2���������ͳ��ͼ������B��Բ�ĽǶ�����
��3������У����2400��ͬѧ������Ƹ�У�������ʻ��ж���ͬѧԼ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʱ����ѧ��ѧ����Ȥ������ʵʩ��������߰���.Ϊ���˽�ѧ����ϲ����һ�������˶����Ա�������Ż���أ���ȫУ����ϲ��һ�����ࣨƹ������ë���������������˶���1200��ѧ���У������ȡ��������ѧ�����е��飨ÿ��ֻ���������������˶���ѡ��һ�֣�.������ͳ�����£�
�������� | ƹ���� | ��ë�� | ���� | ���� | ���� |
���� | 42 |
| 15 | 33 |
|
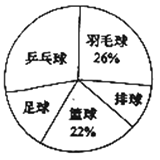
����������⣺
��1����γ��������е�������________��
��2��ͳ�Ʊ��У�![]() ________��
________��![]() ________��
________��
��3���Թ�������1200��ѧ������ϲ��ƹ�����˶�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�ж����Ʒ����װ���ﹲ��45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ���������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ����������4�����ۣ�
�ٿ�ݳ��Ӽص��ҵص��ٶ�Ϊ100ǧ��/ʱ��
�ڼס�������֮��ľ���Ϊ120ǧ�ף�
��ͼ�е�B������Ϊ(![]() ��
��![]() )��
)��
�ܿ�ݳ����ҵط���ʱ���ٶ�Ϊ90ǧ��/ʱ��
����4��������ȷ����________��
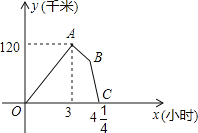
A.�٢ڢۢ�B.�٢ۢ�C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
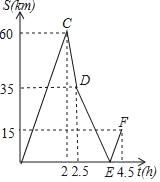
����Ŀ��A��B�������150km���ס��������Ⱥ��A�س�����B����ʻ������Ħ�г�������ʻ���ҿ�������;���ٶ�ֻ�ı�һ�Σ���ͼ��ʾ���Ǽס�������֮��ľ���S����ʱ��t�ĺ���ͼ��F��ʵ���������ҿ���������B�أ��������ͼ�����������⣺
��1��������ٶȣ�
��2�������ǰ�����ε��ٶȣ��������E�����ꣻ
��3�����ס����������10kmʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������![]() �ı߳�Ϊ4,��
�ı߳�Ϊ4,��![]() ����
����![]() �����ģ�
�����ģ�![]() .�Ƶ�
.�Ƶ�![]() ��ת
��ת![]() ,�ֱ��߶�
,�ֱ��߶�![]() ��
��![]() ���㣬����
���㣬����![]() ,���������ĸ�����:��
,���������ĸ�����:��![]() ;��
;��![]() ;���ı���
;���ı���![]() �����ʼ�յ���
�����ʼ�յ���![]() ;�ܡ�
;�ܡ�![]() �ܳ�����СֵΪ6,������������ȷ�ĸ�����( )
�ܳ�����СֵΪ6,������������ȷ�ĸ�����( )
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com