
【题目】已知在平面直角坐标系中,等边△ABC的顶点A、B、C的坐标分别为(a,4)、(b,0)、(c,6),且a<b<c,则等边△ABC的边长为__________.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
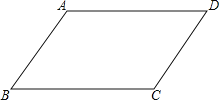
【题目】如图,在平行四边形ABCD中,
(1)以BD为对角线,作菱形MBND,使得M、N分别在BA、DC的延长线上.(保留作图痕迹,不写作图过程)
(2)证明所作四边形MBND是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0) .以D为顶点的抛物线y = ax2+bx+c过点B. 动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒. 过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.

(1)求抛物线的解析式;
(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?
(3)动点P、Q运动过程中,在矩形ABCD内(包括其边界)是否存在点H,使以B,Q,E,H为顶点的四边形是菱形,若存在,请直接写出此时菱形的周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
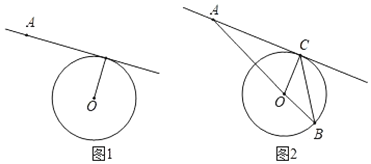
【题目】如图1,点A是⊙O外一点.
(1)过点A作⊙O的切线(要求:尺规作图,保留作图痕迹,不写作法);
(2)如图2,设AC是⊙O的切线,点C是切点,已知tan∠A=![]() ,求tan∠ABC的值.
,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初级中学初一、初二、初三三个年段均有学生500人,为了解数学史知识的普及情况,按年段以2%的比例随机抽样,然后进行模拟测试,测试成绩整理如下:
初一年段 | 36 | 55 | 67 | 68 | 75 | 81 | 81 | 85 | 92 | 96 |
初二年段 | 45 | 66 | 72 | 77 | 80 | 84 | 86 | 92 | 95 | 96 |
初三年段 | 55 | 68 | 75 | 84 | 85 | 87 | 93 | 94 | 96 | 97 |
(1)估计该校学生数学史掌握水平能达到80分以上(含80分)的人数;
(2)现从样本成绩在95分以上(含95分)的学生中,任取3名参加数学史学习的经验汇报,求各年段恰好都有一名学生参加的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
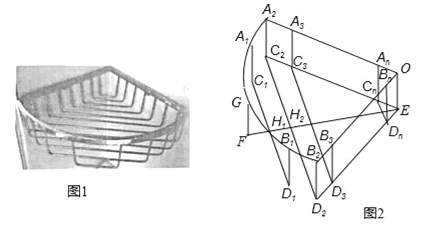
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com