
【题目】早晨![]() 点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离
点,小明乘车从学校出发,去卧龙大熊猫自然保护区参观,当天按原路返回.如图,是小明出行的过程中,他距卧龙大熊猫自然保护区的距离![]() (千米)与他离校的时间
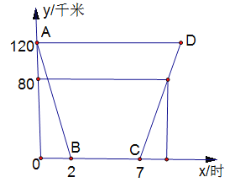
(千米)与他离校的时间![]() (小时)之间的图象.根据图象,完成下面问题:
(小时)之间的图象.根据图象,完成下面问题:
(1)小明乘车去保护区的速度是_________千米/小时,![]() 线段所表示的
线段所表示的![]() 与
与![]() 的关系式是_________;
的关系式是_________;
(2)已知下午![]() 点,小明距保护区
点,小明距保护区![]() 千米,问他何时才能回到学校?
千米,问他何时才能回到学校?
【答案】(1)60,![]() ;(2)下午五点才能回到家
;(2)下午五点才能回到家
【解析】
(1)先根据速度=路程÷时间求出小明乘车去保护区的速度,可设线段AB所表示的函数关系式为:y=kx+b,根据待定系数法列方程组求解即可;
(2)先根据速度=路程÷时间求出小明回家的速度,再根据时间=路程÷速度,列出算式计算即可求解.
解:(1)解:(1)小明乘车去时的平均速度是120÷2=60千米/小时,
设线段AB所表示的函数关系式为:y=kx+b依题意得:![]()
解得:![]()
∴y与x的关系式是y=-60x+120(0≤x≤2).
故答案为: ![]() ;
;![]() (0≤x≤2).
(0≤x≤2).
(2)由图象得小明于7+7=14时(即下午2点)开始返回,
∵下午4点时距离保护区80千米,
∴下午2点到下午4点共2小时,
∴返回的速度为80÷2=40(千米/时),
∴返回共需时间为120÷40=3小时,
∴到家时间为2+3=5(时),
答:他下午5点才能到学校.


科目:初中数学 来源: 题型:
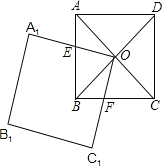
【题目】如图,正方形ABCD的对角线AC和BD相交于点O,O又是正方形A1B1C1O的一个顶点,OA1交AB于点E,OC1交BC于点F.
(1)求证:△AOE≌△BOF;
(2)如果两个正方形的边长都为a,那么正方形A1B1C1O绕O点转动,两个正方形重叠部分的面积等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN. 如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度. 若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动_________秒,两灯的光束互相平行.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为8,
表示的数为8,![]() 是数轴上位于点
是数轴上位于点![]() 左侧一点,且
左侧一点,且![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)数轴上点![]() 表示的数是___________;点
表示的数是___________;点![]() 表示的数是___________(用含
表示的数是___________(用含![]() 的代数式表示)
的代数式表示)
(2)动点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点![]() 同时出发,问多少秒时
同时出发,问多少秒时![]() 之间的距离恰好等于2?
之间的距离恰好等于2?
(3)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,在点
的中点,在点![]() 运动的过程中,线段
运动的过程中,线段![]() 的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段
的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段![]() 的长.
的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点( ![]() ,0),有下列结论:①abc>0;
,0),有下列结论:①abc>0;
②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是( )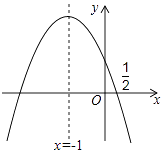
A.①②③
B.①③④
C.①②③⑤
D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市七年级学生对数学知识的掌握情况,在一次数学检测中,从全市2000名年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:

(1)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() ,
,![]() ;
;
(2)请在图中补全频数分布直方图;
(3)如果把成绩在100分以上(含100分)定为优秀,那么该市2000名七年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是AC的中点,B是线段AC上任意一点,M是AB的中点,N是BC的中点,那么下列四个等式中,不成立的是( )
![]()
A.MN=OCB.MO=![]() (AC-AB)
(AC-AB)
C.ON=![]() (AC - CB)D.MN=
(AC - CB)D.MN=![]() (AC+OB)
(AC+OB)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com