
【题目】如图,△ABC和△ADE均为等边三角形,CE,BD相交于点P,连接PA.

(1)求证:CE=BD;
(2)求证:PA平分∠BPE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据等边三角形的性质得出AE=AD,再由∠EAD+∠DAC=∠BAC+∠DAC,得出∠DAB=∠EAC,利用SAS可证得△EAC≌△DAB,从而可得出结论.
(2)根据△EAC≌△DAB可得∠ACF=∠ABE,证明△BAE≌△CAF(AAS),得出AE=AF,即可得出结论.
(1)证明:∵△ABC和△ADE均为等边三角形,

∴AE=AD、AB=AC,
又∵∠EAD=∠BAC=60°,∠EAD+∠DAC=∠BAC+∠DAC,
即∠DAB=∠EAC,
在△EAC和△DAB中,
 ,
,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)证明:作AE⊥BD于E,AF⊥CE于F,如图所示:
则∠BEA=∠CFA=90°,
由(1)得:△EAC≌△DAB,
∴∠ACF=∠ABE,
在△BAE和△CAF中,
 ,
,
∴△BAE≌△CAF(AAS),
∴AE=AF,
∵AE⊥BD于E,AF⊥CE于F,
∴PA平分∠BPE.


科目:初中数学 来源: 题型:
【题目】某幢建筑物,从10米高的窗口A用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),(如图)如果抛物线的最高点M离墙1米,离地面![]() 米,则水流下落点B离墙距离OB是( )
米,则水流下落点B离墙距离OB是( )

A. 2米 B. 3米 C. 4米 D. 5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.
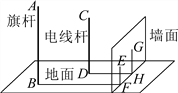
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小,请在图中画出△AMN,写出画图过程并直接写出∠MAN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)过点B作直线![]() 与x轴相交于点P,且使
与x轴相交于点P,且使![]() ,求
,求![]() 的面积.
的面积.
(3)如果x轴上有一动点M,要使以A、B、M为顶点的三角形构成为等腰三角形,请探究并求出符合条件的所有M点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
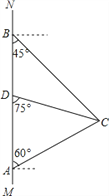
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(2,1),B(-1,n)两点.
的图象交于点A(2,1),B(-1,n)两点.
(1)求反比例函数的解析式;
(2)求一次例函数的解析式;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com