
分析 首先把$\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$=4,两边同乘$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$的数值,再进一步求得($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)的数值即可.
解答 解:∵$\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$=4,
∴($\sqrt{{x}^{2}+25}$-$\sqrt{{x}^{2}-15}$)($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)=4($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$),
∴4($\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$)=40,
∴$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-15}$=10.
点评 此题考查二次根式的化简求值,注意式子的特点,灵活运用平方差公式解决问题,注意整体思想的渗透.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | ${(1+x)^2}=\frac{1}{2}$ | B. | ${(1-x)^2}=\frac{1}{2}$ | C. | (1+x)2=2 | D. | (1-x)2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{5}$,2 | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 3,4,5 | D. | 32,42,52 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
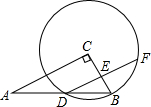 如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,AB=10,若以点C为圆心,CB长为半径的圆恰好经过AB的中点D,弦DF∥AC,则DF的长为5$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com