
【题目】某货站传送货物的平面示意图如图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带![]() 长为
长为![]() .
.

(1)求新传送带的长度;
(2)如果需要在货物着地点![]() 的左侧留出
的左侧留出![]() 的通道,试判断距离点
的通道,试判断距离点![]() 处
处![]() 的货物
的货物![]() 是否需要挪走,并说明理由.(说明:(1),(2)的计算结果精确到
是否需要挪走,并说明理由.(说明:(1),(2)的计算结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)新传送带的长度约为![]() m;(2)货物
m;(2)货物![]() 需要挪走,理由见解析
需要挪走,理由见解析
【解析】
(1)过点A作AD⊥地面于点D,根据锐角三角函数即可求出AD和BD,再根据锐角三角函数即可求出AC和CD即可得出结论;
(2)先求出BC的长,然后即可求出CP的长,最后比较大小即可得出结论.
解:(1)过点A作AD⊥地面于点D
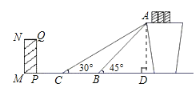
在Rt△ABD中,∠ABD=45°,AB=4m
∴AD= AB·sin∠ABD=![]() m,BD=AB·cos∠ABD=
m,BD=AB·cos∠ABD=![]() m,
m,
在Rt△ACD中,∠ACD=30°
∴AC=2AD=![]() m≈
m≈![]() m,CD=
m,CD=![]() m
m
答:新传送带的长度约为![]() m.
m.
(2)货物![]() 需要挪走,理由如下
需要挪走,理由如下
由(1)知,BD=![]() m,CD=
m,CD=![]() m,
m,
∴BC=(![]() -
-![]() )m
)m
由题意可知BP=4m
∴CP=BP-BC=(4-![]() +
+![]() )m≈
)m≈![]() m<2m
m<2m
∴货物![]() 需要挪走.
需要挪走.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知甲、乙两个长方形纸片,其边长如图中所示![]() ,面积分别为
,面积分别为![]() 和
和![]() .
.

(1)①用含![]() 的代数式表示
的代数式表示![]() _________,
_________,![]() _________;
_________;
②用“![]() ”、“
”、“![]() ”或“
”或“![]() ”号填空:
”号填空:![]() ________
________![]() ;
;
(2)若一个正方形纸片的周长与乙的周长相等,其面积设为![]() .
.
①该正方形的边长是_________(用含![]() 的代数式表示);
的代数式表示);
②小方同学发现,“![]() 与
与![]() 的差是定值”请判断小方同学的发现是否正确,并通过计算说明你的理由.
的差是定值”请判断小方同学的发现是否正确,并通过计算说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
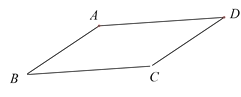
【题目】在ABCD中,∠D=30°,AB<AD.
(1)在AD边上求作一点P,使点P到边AB,BC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接BP,若AB=2,求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式一一利用函数图象研究其性质一一运用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象.同时,我们也学习了绝对值的意义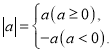 结合上面经历的学习过程,现在来解决下面的问题:在函数
结合上面经历的学习过程,现在来解决下面的问题:在函数![]() 中,当
中,当![]() 时,
时,![]() .
.
(1)求这个函数的表达式;
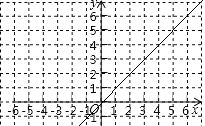
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;
(3)已如函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为( )
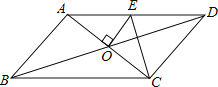
A. 8cmB. 9cmC. 10cmD. 11cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AM∥BN,C是BN上一点, BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.

(1)求证:△ADO≌△CBO.
(2)求证:四边形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com