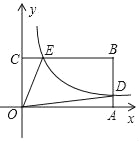
[题目]如图.在以O为原点的直角坐标系中.点A.C分别在x轴.y轴的正半轴上.点B在第一象限内.四边形OABC是矩形.反比例函数y＝(x＞0)与AB相交于点D.与BC相交于点E.若BE＝4CE.四边形ODBE的面积是8.则k＝．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在以O为原点的直角坐标系中，点A，C分别在x轴、y轴的正半轴上，点B在第一象限内，四边形OABC是矩形，反比例函数y＝（x＞0）与AB相交于点D，与BC相交于点E，若BE＝4CE，四边形ODBE的面积是8，则k＝_____．

【答案】2

【解析】

利用反比例函数图象上点的坐标特征，设E（a，），利用BE=4CE得到B（5a，），根据反比例函数比例系数k的几何意义，利用四边形ODBE的面积=S矩形ABCO-S△OCE-S△AOD得到5a-k-k=8，然后解方程即可．

设E（a，），

∵BE=4CE，

∴B（5a，），

∵四边形ODBE的面积=S矩形ABCO-S△OCE-S△AOD，

∴5a-k-k=8，

解得k=2．

故答案为2．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，∠C=90°， AD是∠BAC的平分线，O是AB上一点, 以OA为半径的⊙O经过点D．

（1）求证：BC是⊙O切线；

（2）若BD=5，DC=3，求AC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，AB是⊙O 的直径，CD是⊙O的一条弦，且CD⊥AB于点E．

（1）求证：∠BCO=∠D；

（2）若CD=，AE=2，求⊙O的半径．

查看答案和解析>>

科目：初中数学 来源： 题型：

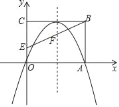
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在x轴、y轴的正半轴上，且OA＝4，OC＝3，若抛物线经过O，A两点，且顶点在BC边上，点E的坐标分别为（0，1），对称轴交BE于点F．

（1）求该抛物线的表达式；

（2）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，AB＝AC，若将△ABC绕点C顺时针旋转180°得到△EFC，连接AF、BE．

（1）求证：四边形ABEF是平行四边形；

（2）当∠ABC为多少度时，四边形ABEF为矩形？请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，在Rt△ABC中，∠ACB＝90°，BC＝4，AB＝4，点D是AC边上的一个动点，将△ABD沿BD所在直线折叠，使点A落在P处．

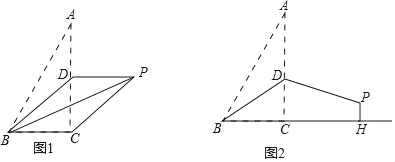
（1）如图1，若点D是AC中点，连接PC．

①求AC的长；

②试猜想四边形BCPD的形状，并加以证明；

（2）如图2，若BD＝AD，过点P作PH⊥BC交BC的延长线于点H，求CH的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

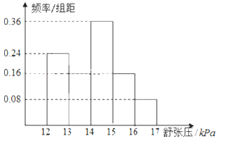
【题目】为了研究某药品的疗效，现选取若干名志愿者进行临床试验．所有志愿者的舒张压数据（单位：kPa）的分组区间为[12，13），[13，14），[14，15），[15，16），[16，17]，将其按从左到右的顺序分别编号为第一组、第二组、…、第五组．如图是根据试验数据制成的频率分布直方图．

（1）若第一组接受治疗的志愿者有12人，则第三组接受治疗的志愿者有多少人？

（2）若接受治疗的志愿者共有50人，规定舒张压在14kpa以上的志愿者接受进一步的临床试验，若从三组志愿者中按比例分配20张床位，则舒张压数据在[14，15）的志愿者总共可以得到多少张床位？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某商家销售一款商品，进价每件80元，售价每件145元，每天销售40件，每销售一件需支付给商场管理费5元，未来一个月按30天计算，这款商品将开展“每天降价1元”的促销活动，即从第一天开始每天的单价均比前一天降低1元，通过市场调查发现，该商品单价每降1元，每天销售量增加2件，设第x天且x为整数的销售量为y件．