
如图,抛物线与x轴交于点A(﹣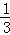 ,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣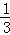 <t<2),求△ABN的面积S与t的函数关系式;
<t<2),求△ABN的面积S与t的函数关系式;
(3)若﹣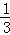 <t<2且t≠0时△OPN∽△COB,求点N的坐标.
<t<2且t≠0时△OPN∽△COB,求点N的坐标.
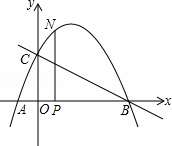
解:(1)设抛物线的解析式为y=ax2+bx+c,由题可得:
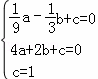 ,
,
解得: ,
,
∴抛物线的函数关系式为y=﹣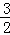 x2+
x2+ x+1;
x+1;
(2)当﹣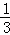 <t<2时,yN>0,
<t<2时,yN>0,
∴NP= =yN=﹣
=yN=﹣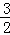 t2+
t2+ t+1,
t+1,
∴S=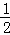 AB•PN
AB•PN
=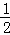 ×(2+
×(2+ )×(﹣
)×(﹣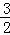 t2+
t2+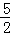 t+1)
t+1)
= (﹣
(﹣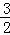 t2+
t2+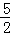 t+1)
t+1)
=﹣ t2+
t2+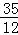 t+
t+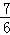 ;
;
(3)∵△OPN∽△COB,
∴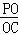 =
=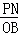 ,
,
∴ =
=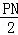 ,
,
∴PN=2PO.
①当﹣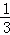 <t<0时,PN=
<t<0时,PN=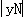 =yN=﹣
=yN=﹣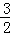 t2+
t2+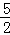 t+1,PO=
t+1,PO= =﹣t,
=﹣t,
∴﹣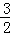 t2+
t2+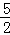 t+1=﹣2t,
t+1=﹣2t,
整理得:3t2﹣9t﹣2=0,
解得:t1=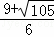 ,t2=
,t2=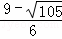 .
.
∵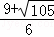 >0,﹣
>0,﹣ <
<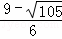 <0,
<0,
∴t=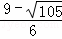 ,此时点N的坐标为(
,此时点N的坐标为(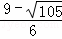 ,
,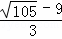 );
);
②当0<t<2时,PN=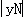 =yN=﹣
=yN=﹣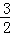 t2+
t2+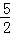 t+1,PO=
t+1,PO= =t,
=t,
∴﹣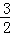 t2+
t2+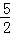 t+1=2t,
t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣ ,t4=1.
,t4=1.
∵﹣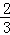 <0,0<1<2,
<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
综上所述:点N的坐标为( ,
,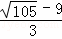 )或(1,2).
)或(1,2).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
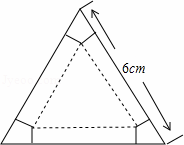
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
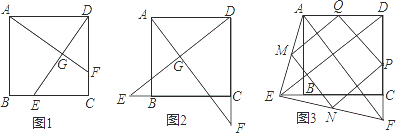
已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为 边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
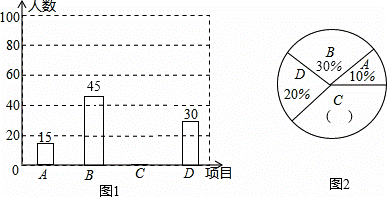
为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com