练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

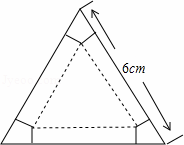
    如图，有一块边长为6cm的正三角形纸板，在它的三个角处分别截去一个彼此全等的筝形，再沿图中的虚线折起，做成一个无盖的直三棱柱纸盒，则该纸盒侧面积的最大值是（　　）

    　

    A．

    cm2

    B．

    cm2

    C．

    cm2

    D．

    cm2


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，数轴上表示的是某个函数自变量的取值范围，则这个函数解析式为（　　）

    　

    A．

    y=x+2

    B．

    y=x2+2

    C．

    y=

    D．

    y=

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    手工课上，老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形，聪明的你请在下列四个正方形中画出不同的剪裁线，并直接写出每种不同分割后得到的最小等腰直角三角形面积（注：不同的分法，面积可以相等）

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是（　　）

    　

    A．

    +=

    B．

    3x2y﹣x2y=3

    　

    C．

    =a+b

    D．

    （a2b）3=a6b3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


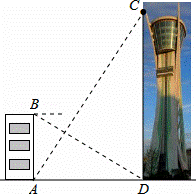
    观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是　　m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．

    （1）求证：DE⊥AG；

    （2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．

    ①在旋转过程中，当∠OAG′是直角时，求α的度数；

    ②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解不等式x＞x﹣2，并将其解集表示在数轴上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，抛物线与x轴交于点A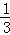（﹣，0）、点B（2，0），与y轴交于点C（0，1），连接BC．

    （1）求抛物线的函数关系式；

    （2）点N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t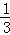（﹣＜t＜2），求△ABN的面积S与t的函数关系式；

    （3）若﹣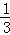＜t＜2且t≠0时△OPN∽△COB，求点N的坐标．

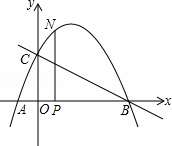
    查看答案和解析>>

    同步练习册答案