
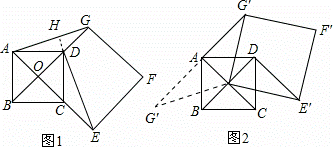
如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.

解:(1)如图1,延长ED交AG于点H,
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∵OG=OE,
在△AOG和△DOE中,
 ,
,
∴△AOG≌△DOE,
∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,
∴∠AGO+∠DEO =90°,
=90°,
∴∠AHE=90°,
即DE⊥AG;
(2)①在旋转过程中,∠OAG′成为直角有两种情况:
(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD= OG=
OG= OG′,
OG′,
∴在Rt△OAG′中,sin∠AG′O= =
= ,
,
∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,
∴OD∥AG′,
∴∠DOG′=∠AG′O=30°,
即α=30°;
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,
∴α=180°﹣30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②如图3,当旋转到A、O、F′在一条直线上时,AF′的长最大,
∵正方形ABCD的边长为1,
∴OA=OD=OC=OB= ,
,
∵OG=2OD,
∴OG′=OG= ,
,
∴OF′=2,
∴AF′=AO+OF′=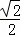 +2,
+2,
∵∠COE′=45°,
∴此时α=315°.



科目:初中数学 来源: 题型:
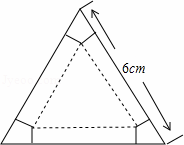
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
正比例函数y1=mx(m>0)的图象与反比例函数y2=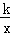 (k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是
(k≠0)的图象交于点A(n,4)和点B,AM⊥y轴,垂足为M.若△AMB的面积为8,则满足y1>y2的实数x的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为 边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
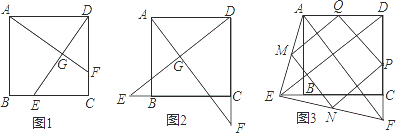
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;
(3)如图3,在(2)的基础上,连接AE和BF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com