
【题目】如图,直线PQ∥MN,点C是PQ、MN之间(不在直线PQ,MN上)的一个动点.
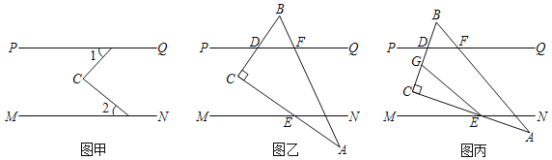
(1)若∠1与∠2都是锐角,如图甲,请直接写出∠C与∠1,∠2之间的数量关系;
(2)若把一块三角尺(∠A=30°,∠C=90°)按如图乙方式放置,点D,E,F是三角尺的边与平行线的交点,若∠AEN=∠A,求∠BDF的度数;
(3)将图乙中的三角尺进行适当转动,如图丙,直角顶点C始终在两条平行线之间,点G在线段CD上,连接EG,且有∠CEG=∠CEM,求![]() 值.
值.
【答案】(1)∠C=∠1+∠2,理由见解析;(2)60°;(3)2
【解析】
(1)过C作CD∥PQ,依据平行线的性质,即可得出∠C=∠1+∠2;
(2)根据(1)中的结论可得,∠C=∠MEC+∠PDC=90°,再根据对顶角相等即可得出结论;
(3)设∠CEG=∠CEM=x,得到∠GEN=180°2x,再根据(1)中的结论可得∠CDP=90°∠CEM=90°x,再根据对顶角相等即可得出∠BDF=90°x,据此可得![]() 的值.
的值.
(1)∠C=∠1+∠2.
理由:如图,过C作CD∥PQ,

∵PQ∥MN,
∴PQ∥CD∥MN,
∴∠1=∠ACD,∠2=∠BCD,
∴∠ACB=∠ACD+∠BCD=∠1+∠2.
(2)∵∠AEN=∠A=30°,
∴∠MEC=30°,
由(1)可得,∠C=∠MEC+∠PDC=90°,
∴∠PDC=90°﹣∠MEC=60°,
∴∠BDF=∠PDC=60°;
(3)设∠CEG=∠CEM=x,则∠GEN=180°﹣2x,
由(1)可得,∠C=∠CEM+∠CDP,
∴∠CDP=90°﹣∠CEM=90°﹣x,
∴∠BDF=90°﹣x,
∴![]() =
=![]() =2.
=2.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E、F分别是AC、BC的中点,直线EF与⊙O交于点G、H.若⊙O的半径为2,则GE+FH的最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦)长为37.4m,拱高(弧的中点到弦的距离)为7.2m,请求出赵州桥的主桥拱半径(结果保留小数点后一位).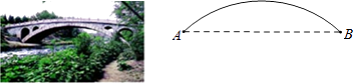
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16min时到家,假设小东始终以100m/min的速度步行,两人离家的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示:
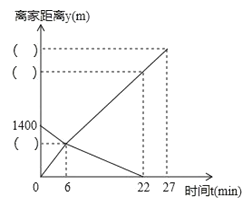
(1)小东打电话时,他离家_________m;
(2)填上图中空格相应的数据_________,_________,_________;
(3)小东和妈妈相遇后,妈妈回家的速度为_________m/min;
(4)_________min时,两人相距700m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法①△ABC中,若∠A+∠B=90°,则△ABC是直角三角形;②已知正n边形的一个内角为140,则这个正多边形的边数是9;③一个多边形的内角中最多有3个锐角;④三角形的外角一定大于内角;⑤若不等式组![]() 的整数解恰好有2个,则m的取值范围是
的整数解恰好有2个,则m的取值范围是![]() ,其中说法正确的是_____________________(填写说法正确的序号)
,其中说法正确的是_____________________(填写说法正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
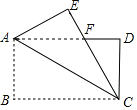
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.
【答案】![]()
【解析】
由矩形的性质可得AB=CD=4,BC=AD=6,AD//BC,由平行线的性质和折叠的性质可得∠DAC=∠ACE,可得AF=CF,由勾股定理可求AF的长,即可求△AFC的面积.
解:![]() 四边形ABCD是矩形
四边形ABCD是矩形
![]() ,
,![]() ,
,![]()
![]() ,
,
![]() 折叠
折叠
![]() ,
,
![]()
![]()
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
![]() .
.
故答案为:![]() .
.
【点睛】
本题考查了翻折变换,矩形的性质,勾股定理,利用勾股定理求AF的长是本题的关键.
【题型】填空题
【结束】
12
【题目】某公司要招聘一名新的大学生,公司对入围的甲、乙两名候选人进行了三项测试,成绩如表所示,根据实际需要,规定能力、技能、学业三项测试得分按5:3:2的比例确定个人的测试成绩,得分最高者被录取,此时______将被录取.
得分 | 能力 | 技能 | 学业 |
甲 | 95 | 84 | 61 |
乙 | 87 | 80 | 77 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一次函数y=(a+1)x+(a﹣4)的图象不经过第二象限,且关于x的分式方程![]() 有整数解,那么整数a值不可能是( )
有整数解,那么整数a值不可能是( )
A. 0B. 1C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com