
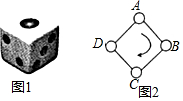
 如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字1,2,3,4,5,6,如图2,正方形ABCD的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落在圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落得圈B;…设游戏者从圈A起跳.
如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字1,2,3,4,5,6,如图2,正方形ABCD的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落在圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落得圈B;…设游戏者从圈A起跳.分析 (1)由共有6种等可能的结果,落回到圈A的只有1种情况,直接利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与最后落回到圈A的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵掷一次骰子有6种等可能的结果,只有掷的4时,才会落回到圈A,
∴落回到圈A的概率P1=$\frac{1}{6}$;
(2)列表得:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;用到的知识点为:概率=所求情况数与总情况数之比.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
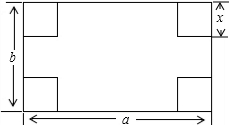 如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.
如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
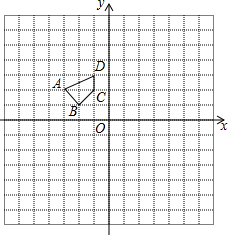 如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在格点上.
如图,在平面直角坐标系中,四边形ABCD的四个顶点分别在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
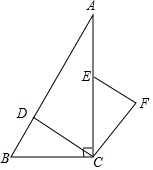 如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com