
分析 可设三个机器人的速度分别为VA、VB、VC,轨道周长为L.则得①:2VA=2VB+L,②:2.5VA=2.5VC+L,③:因为C追上B时,两个所用时间一样,所以路程比等于速度比,即VC:VB=3:2,联立解三式得:2.5VA=1.75L,可由此推出60VA=42L,也就是说60秒时,A机器人运动了42圈.
解答 解:设三个机器人的速度分别为VA、VB、VC,轨道周长为L.依题意有
$\left\{\begin{array}{l}{2{V}_{A}=2{V}_{B}+L}\\{2.5{V}_{A}=2.5{V}_{C}+L}\\{{V}_{C}:{V}_{B}=3:2}\end{array}\right.$,
可得:2.5VA=1.75L,
则60VA=42L.
故第1分钟时,A围绕这个圆形轨道运动了42圈.
点评 考查了应用类问题,本题关键是根据题意得到等量关系:①:2VA=2VB+L;②:2.5VA=2.5VC+L;③VC:VB=3:2.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
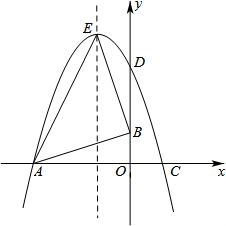 如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.
如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
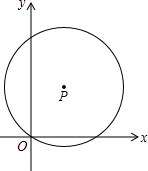 如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
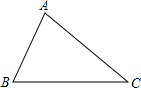 如图,已知△ABC,按下列语句要求用尺规作图(保留作图痕迹,不写作法);
如图,已知△ABC,按下列语句要求用尺规作图(保留作图痕迹,不写作法);查看答案和解析>>
科目:初中数学 来源: 题型:选择题
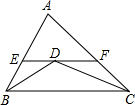 如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com