
���� ��1�������¶���ֱ���м��㣻
��2�����ã�1���еļ�������${C}_{4}^{2}$+${C}_{4}^{3}$=${C}_{5}^{3}$��${C}_{5}^{4}$+${C}_{5}^{5}$=${C}_{6}^{5}$���ɴ˹��ɿɵ�${C}_{n}^{k}$+${C}_{n}^{k+1}$=${C}_{n+1}^{k+1}$��
��3�����ã�2���еĹ��ɴ��������μ��㼴�ɣ�
��� �⣺��1��${C}_{4}^{2}$=$\frac{4��3}{2��1}$=6��${C}_{4}^{3}$=$\frac{4��3��2}{3��2��1}$=4��${C}_{5}^{3}$=$\frac{5��4��3}{3��2��1}$=10��${C}_{5}^{4}$=$\frac{5��4��3��2}{4��3��2��1}$=5��${C}_{5}^{5}$=$\frac{5��4��3��2��1}{5��4��3��2��1}$=1��${C}_{6}^{5}$=$\frac{6��5��4��3��2}{5��4��3��2��1}$=6��
�ʴ�Ϊ6��4��10��5��1��6��
��2��${C}_{n}^{k}$+${C}_{n}^{k+1}$=${C}_{n+1}^{k+1}$��
��3��${C}_{3}^{3}$+${C}_{3}^{2}$+${C}_{4}^{2}$+C52+��+${C}_{20}^{2}$=C43+${C}_{4}^{2}$+C52+��+${C}_{20}^{2}$
=C53+C52+��+${C}_{20}^{2}$
=C63+��+${C}_{20}^{2}$
=C213��
���� ���⿼���˹�����-���ֵı仯�ࣺ����۲졢��ϸ˼�������������ǽ����������ķ���������Ĺؼ��Ƕ��¶�������⣮


 Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
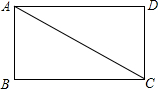 ��֪����ͼ��Rt��ABC��Rt��CDA�����е�A��D�Ķ�Ӧ��ֱ���C��B����B=��D=Rt�ϣ���֤���ı���ABCD�Ǿ��Σ�
��֪����ͼ��Rt��ABC��Rt��CDA�����е�A��D�Ķ�Ӧ��ֱ���C��B����B=��D=Rt�ϣ���֤���ı���ABCD�Ǿ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
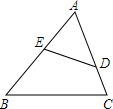 ��ͼ��D��E�ֱ��ǡ�ABC�ı�AC��AB�ϵĵ㣬AD=6��AB=10��BC=12����$\frac{AE}{AC}=\frac{3}{5}$��
��ͼ��D��E�ֱ��ǡ�ABC�ı�AC��AB�ϵĵ㣬AD=6��AB=10��BC=12����$\frac{AE}{AC}=\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
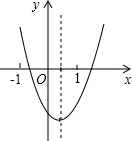 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����abc��b2-4ac��2a+b��a+b+c���ĸ�ʽ���У�ֵΪ�������У�������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����abc��b2-4ac��2a+b��a+b+c���ĸ�ʽ���У�ֵΪ�������У�������| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 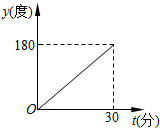 | ||
| C�� | 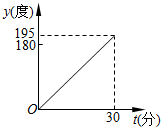 | D�� | 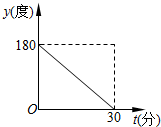 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com