

分析 (1)根据与x轴的两个交点A、B的坐标,设出二次函数交点式解析式y=a(x+1)(x-2),然后把点C的坐标代入计算求出a的值,即可得到二次函数解析式;
(2)分两种情况:若OC为平行四边形的边;若OC为平行四边形的对角线,可求点Q的坐标;
(3)根据相似三角形对应角相等可得∠MCH=∠CAO,然后分(i)点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是-2,代入抛物线解析式计算即可;(ii)点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标.
解答 解:(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-1,0),B(2,0),
∴设该二次函数的解析式为:y=a(x+1)(x-2),又二次函数y=ax2+bx+c的图象交y轴于C(0,-2),将x=0,y=-2代入,得-2=a(0+1)(0-2),
解得a=1.
∴抛物线的解析式为y=(x+1)(x-2),即y=x2-x-2;
(2)若OC为平行四边形的边,设P(p,p2-p-2),Q(p,p),
则PQ=|p2-2p-2|,P、Q、O、C为顶点的四边形为平行四边形,
则|p2-2p-2|=2,
解得p1=0(舍去),p2=2,${p_3}=1+\sqrt{5}$,${p_4}=1-\sqrt{5}$;
则Q1(2,2),Q2( $1+\sqrt{5}$,$1+\sqrt{5}$),Q3($1-\sqrt{5}$,$1-\sqrt{5}$);
若OC为平行四边形的对角线,则Q4(-2,-2).
(3)∵△CHM∽△AOC,点C与点A对应,∴∠MCH=∠CAO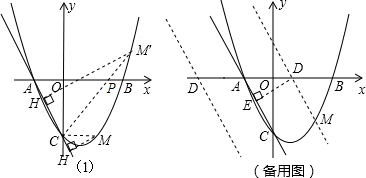 情形1:如图1,当H在点C下方时,
情形1:如图1,当H在点C下方时,
∵∠MCH=∠CAO
∴CM∥x轴,
∴yM=-2,点M在二次函数图象上,
∴x2-x-2=-2,
解得x=0(舍去)或x=1,
∴M(1,-2);
情形2:如图,当H在点C上方时,
∵∠M′CH=∠CAO,
设CM′交x轴于点P,
设OP=x,则PC=PA=x+1,
在Rt△POC中,OP=x,PC=x+1,OC=2
由勾股定理,得x2+22=(x+1)2,
解得$x=\frac{3}{2}$,即$OP=\frac{3}{2}$,
M′为直线CP与抛物线的另一交点,
设直线CM′的解析式为y=kx-2,把$P(\frac{3}{2},0)$的坐标代入,得$\frac{3}{2}k-2=0$,
解得$k=\frac{4}{3}$,
∴$y=\frac{4}{3}x-2$,由$\frac{4}{3}x-2={x^2}-x-2$,
解得x=0(舍去)或$x=\frac{7}{3}$
此时$y=\frac{10}{9}$,
∴$M'(\frac{7}{3},\frac{10}{9})$,
∴点M的坐标为(1,-2)或$(\frac{7}{3},\frac{10}{9})$.
点评 考查了二次函数综合题,主要利用了待定系数法求二次函数解析式,相似三角形的性质,两函数图象交点的求解方法,综合性较强,难度较大,要注意分情况讨论求解.


科目:初中数学 来源: 题型:解答题
| 数量/千克 | 单价/(元/千克) | 销售收入/元 | |
| 甲种糖果 | x | 20 | 20x |
| 乙种糖果 | 200-x | 15 | 15(200-x) |
| 丙种糖果 | 200 | 18 | 200×18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
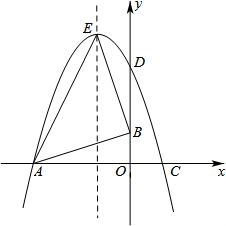 如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.
如图,在直角坐标系中,O是坐标原点,已知△OAB的顶点A(-6,0),B(0,2),将△OAB绕点O按顺时针旋转90°,得到△ODC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
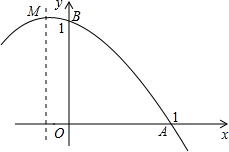 二次函数y=ax2+bx+c的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)此二次函数的图象与x轴的另一个交点为C.
二次函数y=ax2+bx+c的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1)此二次函数的图象与x轴的另一个交点为C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
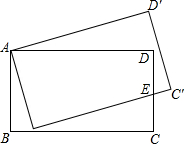 如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.
如图所示,将矩形ABCD旋转到AB′C′D′位置,使边BC恰好经过边CD的中点E.若AB=8,C′E=2,则四边形AB′ED的面积是70.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
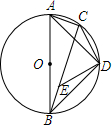 已知:如图,AB是△ABC的外接圆O的直径,D为⊙O上一点,且DE⊥CD,交BC于点E.求证:$\frac{AC}{BE}=\frac{CD}{ED}$.
已知:如图,AB是△ABC的外接圆O的直径,D为⊙O上一点,且DE⊥CD,交BC于点E.求证:$\frac{AC}{BE}=\frac{CD}{ED}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com