
【题目】已知关于x的一元二次方程x2﹣(m+1)x+ ![]() (m2+1)=0有实数根.
(m2+1)=0有实数根.
(1)求m的值;
(2)先作y=x2﹣(m+1)x+ ![]() (m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(m2+1)的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求n2﹣4n的最大值和最小值.
【答案】
(1)解:对于一元二次方程x2﹣(m+1)x+ ![]() (m2+1)=0,
(m2+1)=0,
△=(m+1)2﹣2(m2+1)=﹣m2+2m﹣1=﹣(m﹣1)2,
∵方程有实数根,
∴﹣(m﹣1)2≥0,
∴m=1.
(2)解:由(1)可知y=x2﹣2x+1=(x﹣1)2,
图象如图所示:

平移后的解析式为y=﹣(x+2)2+2=﹣x2﹣4x﹣2.
(3)解:由 ![]() 消去y得到x2+6x+n+2=0,
消去y得到x2+6x+n+2=0,
由题意△≥0,
∴36﹣4n﹣8≥0,
∴n≤7,
∵n≤m,m=1,
∴1≤n≤7,
令y′=n2﹣4n=(n﹣2)2﹣4,
∴n=2时,y′的值最小,最小值为﹣4,
n=7时,y′的值最大,最大值为21,
∴n2﹣4n的最大值为21,最小值为﹣4.
【解析】(1)由题意△≥0,列出不等式,解不等式即可;(2)画出翻折.平移后的图象,根据顶点坐标即可写出函数的解析式;(3)首先确定n的取值范围,利用二次函数的性质即可解决问题;
【考点精析】掌握求根公式和二次函数图象的平移是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.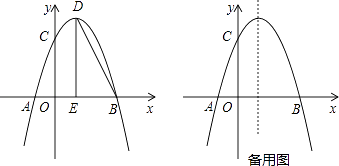
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示点A向右平移1个单位长度,再向下平移2个单位长度得到点A′.
根据上述定义,探究下列问题:
(1)已知点A(x,y),A′(x-3,y),则线段AA′的长度是多少;
(2)已知点A(x,y),A′(x+2,y-1),则线段AA′的长度是多少;
(3)长方形AOCB在平面直角坐标系中的位置如图所示,A(0,2),C(4,0),点A′(x′,y′),若x′=x+m,y′=y-2m(m均为正数),点A′(x′,y′)能否在△OCB的直角边上?若能,求m的值;若不能,请说明理由.
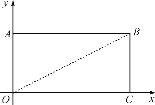
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探索:
(1)已知一个分数![]() ,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
,如果分子、分母同时增加1,分数的值是增大还是减小?请说明你的理由.
(2)若正分数![]() 中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
中分子和分母同时增加2,3,…,k(整数k>0),情况如何?
(3)请你用上面的结论解释下面的问题:
建筑学规定:民用住宅窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,问:同时增加相等的窗户面积和地板面积,住宅的采光条件是变好了,还是变坏了?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 . 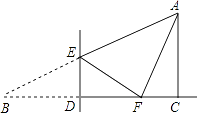
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;
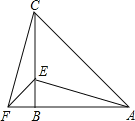
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.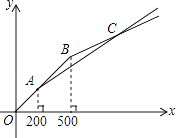
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com