
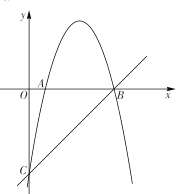
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() .
.
(1)求抛物线的解析式;
(2)![]() 是直线
是直线![]() 上方的抛物线上一动点,求
上方的抛物线上一动点,求![]() 的最大面积.
的最大面积.
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学位为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表.
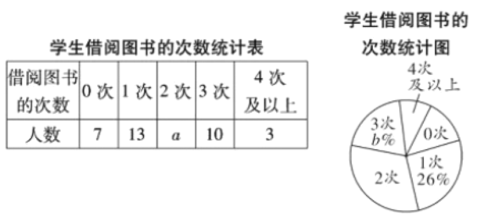
请你根据统计图表中的信息,解答下列问题:
(1)![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)该调查统计数据的中位数是_________,众数是__________;
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,越来越多的人们关注运动与健康,近来“微信运动”逐渐被大家关注和喜爱.某兴趣小组为了了解某社区居民的“微信运动”情况,进行了随机抽样调查,对他们一日“微信运动”中的步数进行了统计,下面给出部分信息:
①
| 频数 | 频率 |
| 5 |
|
| 10 | 0.2 |
| 15 | 0.3 |
|
| 0.2 |
| 8 | 0.16 |
| 2 | 0.04 |
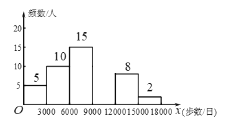
![]() 这一组的数据为:
这一组的数据为:
6000 6200 6200 6500 6600 6800 7000 7200 7200 7200 7800 8000 8300 8700 8900
根据以上信息,回答下列问题:
(1)本次被调查的居民有__________人:表中![]() ______________,
______________,![]() ___________;
___________;
(2)补全频数分布直方图;
(3)直接写出被调查的居民在“微信运动”中步数的中位数;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为 1 ,
的边长为 1 , ![]() 是对角线 . 将
是对角线 . 将![]() 绕着点 D 顺时针旋转
绕着点 D 顺时针旋转![]() 得到
得到![]() 交
交![]() 于点 E ,连接
于点 E ,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() . 下列结论: ①
. 下列结论: ①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() . 其中结论正确的个数是( )
. 其中结论正确的个数是( )
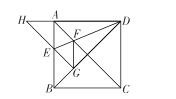
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
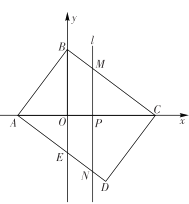
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 动点
动点![]() 从原点出发,以每秒 1 个单位长度的速度沿
从原点出发,以每秒 1 个单位长度的速度沿![]() 轴正方向移动,移动时间为
轴正方向移动,移动时间为![]() 秒,过点 P 作垂直于
秒,过点 P 作垂直于![]() 轴的直线
轴的直线![]() ,交
,交![]() 于点 M ,交
于点 M ,交![]() 或
或![]() 于点 N ,直线
于点 N ,直线![]() 扫过矩形
扫过矩形![]() 的面积为
的面积为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 移动过程中到点
移动过程中到点![]() 之前的
之前的![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在直线![]() 移动过程中,第一象限的直线
移动过程中,第一象限的直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 是等腰直角三角形? 若存在,直接写出点
是等腰直角三角形? 若存在,直接写出点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
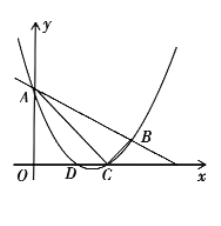
【题目】如图,抛物线![]() 与直线
与直线![]() 交于
交于![]() 两点,交
两点,交![]() 轴与
轴与![]() 两点,连接
两点,连接![]() 已知
已知![]() .
.
(1)求抛物线的解析式;
(2)求证:![]() 是直角三角形;
是直角三角形;
(3)![]() 为
为![]() 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,问:是否存在点
,问:是否存在点![]() 使得以
使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
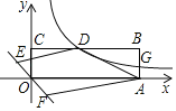
【题目】如图,反比例函数y=![]() (x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
(x>0)的图象与矩形ABCO的边AB交于点G,与边BC交于点D,过点A,D作DE//AF,交直线y=kx(k<0)于点E,F,若OE=OF,BG=2GA,则四边形ADEF的面积为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
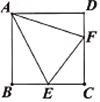
【题目】如图,正方形ABCD边长为6,E是BC的中点,连接AE,以AE为边在正方形内部作∠EAF=45°,边![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则下列说法中:①
,则下列说法中:①![]() ;②
;②![]() ;③tan∠AFE=3;④
;③tan∠AFE=3;④![]() .正确的有( )
.正确的有( )
A.①②③B.②④C.①④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com