
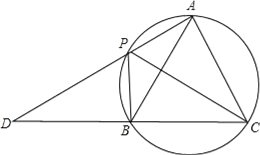
【题目】如图,四边形APBC是圆内接四边形,∠APB=120°,PC平分∠APB,AP,CB的延长线相交于点D.
(1)求证:△ABC是等边三角形;
(2)若∠PAC=90°,AB=2![]()
①求PD的长.
②图中弧BP和线段DP、BD组成的图形面积为 (结果保留π)
【答案】(1)证明见解析;(2)①4;②3![]() ﹣
﹣![]() π.
π.
【解析】分析:(1)根据角平分线的定义结合∠APB=120°可得出∠BPC=60°,利用圆周角定理可求出∠BAC=60°,再根据圆内接四边形的性质可得出∠ACB=60°,由此即可证出△ABC是等边三角形;
(2)①通过解含30度角的直角三角形可求出AP、AD的长度,二者做差即可得出PD的长;
②根据圆内接四边形的性质找出∠PBC=90°,取PC的中点O,连接OB,过点O作OE⊥BC于点E,利用分割图形求面积法即可求出弧BP和线段DP、BD组成的图形面积.
本题解析:
(1)证明:∵∠APB=120°,PC平分∠APB,
∴∠BPC=∠APC=![]() ∠APB=60°,
∠APB=60°,
∴∠BAC=∠BPC=60°.
∵四边形APBC是圆内接四边形,∠APB=120°,
∴∠ACB=180°﹣∠APB=60°,
∴△ABC是等边三角形.
(2)解:①在Rt△PAC中,∠APC=60°,∠PAC=90°,AC=AB=2![]() ,
,
∴∠PCA=30°,
∴PC=2PA.
∵PC2=PA2+AC2,
∴PA=2,PC=4.
同理,可求出CD=4![]() ,AD=6,
,AD=6,
∴PD=AD﹣PA=4.
②∵∠PAC=90°,四边形APBC是圆内接四边形,
∴∠PBC=90°.
取PC的中点O,连接OB,过点O作OE⊥BC于点E,如图所示,
∴PO=![]() PC=2,OE=
PC=2,OE=![]() PB=
PB=![]() PA=1,
PA=1,
∴弧BP和线段DP、BD组成的图形面积=S△PCD﹣S△OBC﹣S扇形POB=![]() ×4
×4![]() ×2﹣
×2﹣![]() ×2
×2![]() ×1﹣
×1﹣![]() π×22=3
π×22=3![]() ﹣
﹣![]() π.
π.
故答案为:3![]() ﹣
﹣![]() π.
π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
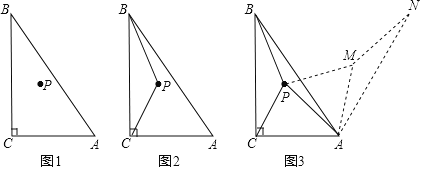
【题目】如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、
A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,
AB=6时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
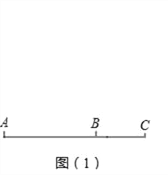
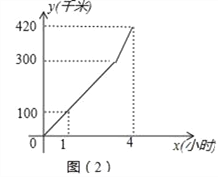
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销店经销一种建筑材料,当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需成本及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)求出y与x的函数关系式(不要求写出x的取值范围);
(2)该经销店要获得最大月利润,售价应定为每吨多少元;
(3)小王说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com