
【题目】如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
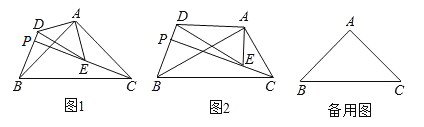
(1)问题提出:如图1,若AD=AE,AB=AC.
①∠ABD与∠ACE的数量关系为 ;②∠BPC的度数为 .
(2)猜想论证:如图2,若∠ADE=∠ABC=30°,则(1)中的结论是否成立?请说明理由.
(3)拓展延伸:在(1)的条件中,若AB=2,AD=1,若把△ADE绕点A旋转,当∠EAC=90°时,直接写出PB的长.
【答案】(1)①∠ABD=∠ACE,②90°;(2)(1)中结论成立,见解析;(3)PB的长为![]() 或
或![]() .
.
【解析】
(1)①依据等腰三角形的性质得到AB=AC,AD=AE,依据同角的余角相等得到∠DAB=∠CAE,然后依据“SAS”可证明△ADB≌△AEC,最后,依据全等三角形的性质可得到∠ABD=∠ACE;
②由三角形内角和定理可求∠BPC的度数;
(2)先判断出△ADB∽△AEC,即可得出结论;
(3)分为点E在AB上和点E在AB的延长线上两种情况画出图形,然后再证明△PEB∽△AEC,最后依据相似三角形的性质进行证明即可.
(1)①∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠DAB=∠CAE.∠ABC=∠ACB=45°,
∴△ADB≌△AEC(SAS),
∴∠ABD=∠ACE.
②∵∠BPC=180°﹣∠ABD﹣∠ABC﹣∠BCP=180°﹣45°﹣(∠BCP+∠ACE),∴∠BPC=90°.
故答案为:∠ABD=∠ACE,90°.
(2)(1)中结论成立,理由如下:
在Rt△ABC中,∠ABC=30°,
∴AB![]() AC.
AC.
在Rt△ADE中,∠ADE=30°,
∴AD![]() AE,
AE,
∴![]() .
.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∴△ADB∽△AEC,
∴∠ABD=∠ACE;
∵∠BPC=180°﹣∠ABD﹣∠ABC﹣∠BCP=180°﹣30°﹣(∠BCP+∠ACE),∴∠BPC=90°;
(3)①如图,当点E在AB上时,BE=AB﹣AE=1.

∵∠EAC=90°,
∴CE![]() .
.
同(1)可证△ADB≌△AEC,
∴∠DBA=∠ECA.
又∵∠PEB=∠AEC,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB![]() ;
;
②如图,当点E在BA延长线上时,BE=AB+AE=3.

∵∠EAC=90°,
∴CE![]() .
.
同(1)可证△ADB≌△AEC,
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB![]() .
.
综上所述:PB的长为![]() 或
或![]() .
.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
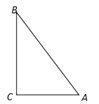
【题目】新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在RtΔABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为 ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 m,n 相交于 O,所夹的锐角是 53°,点 P,Q 分别是直线 m,n上的点,将直线 m,n 按照下面的程序操作,能使两直线平行的是( )

A. 将直线 m 以点 O 为中心,顺时针旋转 53° B. 将直线 n 以点 Q 为中心,顺时针旋转 53°
C. 将直线 m 以点 P 为中心,顺时针旋转 53° D. 将直线 m 以点 P 为中心,顺时针旋转 127°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店以每件40元的价格购进一批衬衫,在试销过程中统计发现,每月的销售量y(件)与销售单价x(其中x为正整数,且50≤x≤75)(元)之间有下表关系:
销售单价x(元) | 50 | 55 | 60 | 65 | 70 | 75 |
每月销售量y(件) | 160 | 140 | 120 | 100 | 80 | 60 |
(1)若y与x之间的函数关系是下列函数关系之一,则y是x的______
A.正比例函数 B.一次函数 C.反比例函数 D.二次函数
(2)求y与x的函数关系式;
(3)如果不考虑其它费用,该店销售这种衬衫的月利润为1600元,这种衬衫的销售单价应定为多少元?
(4)如果每销售一件衬衫需要支出各种费用2元,设服装店每月销售这种衬衫获利为w元,销售单价为多少元时,服装店获利w最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
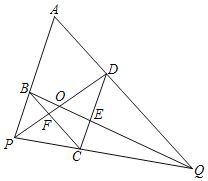
【题目】如图, 已知菱形![]() ,
,![]() ,点
,点![]() 是边
是边![]() 延长线上一点, 连接
延长线上一点, 连接![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式, 并写出它的定义域;
的函数解析式, 并写出它的定义域;
(3)当![]() 与
与![]() 相似时, 求
相似时, 求![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.
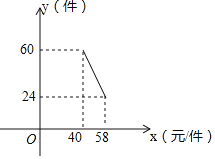
(1)求日销售量y与销售价x之间的函数关系式,并写出x的取值范围;
(2)该品牌服装售价x为多少元时,每天的销售利润W最大,且最大销售利润W为多少?
(3)若该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).现该店只有2名员工,则该店至少需要多少天才能还清所有贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
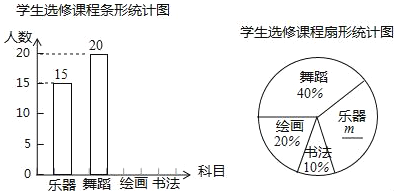
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。
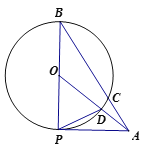
(1)求证:PO=PD
(2)若AC=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com