
ЁОЬтФПЁПЙњМвжЇГжДѓбЇЩњДДаТАьЪЕвЕЃЌЬсЙЉаЁЖюЮоЯЂДћПюЃЌбЇЩњЭѕССЯэЪмЙњМвеўВпДћПю36000дЊгУгкДњРэФГЦЗХЦЗўзАЯњЪлЃЌвбжЊИУЕъДњРэЕФЦЗХЦЗўзАЕФНјМлЮЊУПМў40дЊЃЌИУЦЗХЦЗўзАЪлСПyЃЈМўЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФЙиЯЕПЩгУЭМжаЕФвЛЬѕЯпЖЮЃЈЪЕЯпЃЉРДБэЪОЃЎ
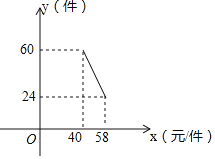
ЃЈ1ЃЉЧѓШеЯњЪлСПyгыЯњЪлМлxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉИУЦЗХЦЗўзАЪлМлxЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓWзюДѓЃЌЧвзюДѓЯњЪлРћШѓWЮЊЖрЩйЃП
ЃЈ3ЃЉШєИУЕъгІжЇИЖдБЙЄЕФЙЄзЪЮЊУПШЫУПЬь82дЊЃЌУПЬьЛЙгІжЇИЖЦфЫќЗбгУЮЊ106дЊЃЈВЛАќКЌДћПюЃЉЃЎЯжИУЕъжЛга2УћдБЙЄЃЌдђИУЕъжСЩйашвЊЖрЩйЬьВХФмЛЙЧхЫљгаДћПюЃП
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ2x+140 ЃЈ40ЁмxЁм58ЃЉЃЛЃЈ2ЃЉЦЗХЦЗўзАЪлМлxЮЊ55дЊЪБЃЌУПЬьЕФЯњЪлРћШѓWзюДѓЃЌЧвзюДѓЯњЪлРћШѓWЮЊ450дЊЃЛЃЈ3ЃЉжСЩйашвЊ200ЬьВХФмЛЙЧхЫљгаДћПю.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтПЩЕУЃЛ
ЃЈ2ЃЉЩшзюДѓРћШѓЮЊWЃЌзмРћШѓ=ЕЅМўРћШѓЁСЯњЪлСПСаГіКЏЪ§НтЮіЪНЃЌгЩЃЈ1ЃЉСаГіЗНГЬМДПЩ
ЃЈ3ЃЉИљОнРћШѓзюДѓжЕЁСЬьЪ§ЁнУПЬьЕФзмжЇГіЁСЬьЪ§+ДћПюЧЎЪ§ЃЌНтВЛЕШЪНПЩЕУД№АИЃЎ
НтЃК
ЃЈ1ЃЉгЩЭМЯѓПЩЕУЃЌЩшШеЯњЪлСПyгыЯњЪлМлxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃКyЃНkx+bЃЌдђга
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЙЪШеЯњЪлСПyгыЯњЪлМлxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃКyЃНЉ2x+140 ЃЈ40ЁмxЁм58ЃЉ
ЃЈ2ЃЉвРЬтвтЃЌЩшзюДѓРћШѓЮЊWЃЌдђга
WЃНЃЈxЉ4ЃЉyЃНЃЈxЉ4ЃЉЃЈЉ2x+140ЃЉЃНЉ2x2+220xЉ5600
ећРэЕУWЃНЉ2ЃЈxЉ55ЃЉ2+450
ЁпХзЮяЯпПЊПкЯђЯТ
ЁрЕБxЃН55ЪБЃЌЛёЕУзюДѓРћШѓ
ЙЪЦЗХЦЗўзАЪлМлxЮЊ55дЊЪБЃЌУПЬьЕФЯњЪлРћШѓWзюДѓЃЌЧвзюДѓЯњЪлРћШѓWЮЊ450дЊ
ЃЈ3ЃЉгЩЬтвтЃЌЩшжСЩйашвЊmЬьВХФмЛЙЧхЫљгаДћПю
гЩга450mЉЃЈ82mЁС2+106mЃЉЁн36000
НтЕУmЁн200
ЙЪжСЩйашвЊ200ЬьВХФмЛЙЧхЫљгаДћПю



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
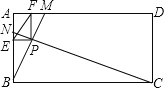
ЁОЬтФПЁПШчЭМЃЌЁїADEШЦе§ЗНаЮABCDЕФЖЅЕуAЫГЪБеыа§зЊ90ЁуЃЌЕУЁїABFЃЌСЌНгEFНЛABгкHЃЌгаШчЯТЮхИіНсТлЂйAEЁЭAFЃЛЂкEFЃКAF=![]() ЃК1ЃЛЂлAF2=FHFEЃЛЂмЁЯAFE=ЁЯDAE+ЁЯCFE Ђн FBЃКFC=HBЃКECЃЎдђе§ШЗЕФНсТлгаЃЈ ЃЉ
ЃК1ЃЛЂлAF2=FHFEЃЛЂмЁЯAFE=ЁЯDAE+ЁЯCFE Ђн FBЃКFC=HBЃКECЃЎдђе§ШЗЕФНсТлгаЃЈ ЃЉ
A.2ИіB.3ИіC.4ИіD.5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвЛИіЩШаЮжНЦЌЕФдВаФНЧЮЊ90ЁуЃЌАыОЖЮЊ6ЃЎШчЭМ2ЃЌНЋетеХЩШаЮжНЦЌелЕўЃЌЪЙЕуAгыЕуOЧЁКУжиКЯЃЌелКлЮЊCDЃЌЭМжавѕгАЮЊжиКЯВПЗжЃЌдђвѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ(Д№АИгУИљКХБэЪО)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
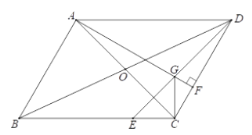
ЁОЬтФПЁПШчЭМЃЌдкЁїABCКЭЁїADEжаЃЌЁЯBACЃНЁЯDAEЃН90ЁуЃЌЕуPЮЊЩфЯпBDЃЌCEЕФНЛЕуЃЎ
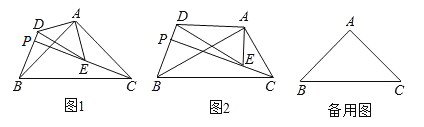
ЃЈ1ЃЉЮЪЬтЬсГіЃКШчЭМ1ЃЌШєADЃНAEЃЌABЃНACЃЎ
ЂйЁЯABDгыЁЯACEЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁЃЛЂкЁЯBPCЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉВТЯыТлжЄЃКШчЭМ2ЃЌШєЁЯADEЃНЁЯABCЃН30ЁуЃЌдђЃЈ1ЃЉжаЕФНсТлЪЧЗёГЩСЂЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЭиеЙбгЩьЃКдкЃЈ1ЃЉЕФЬѕМўжаЃЌШєABЃН2ЃЌADЃН1ЃЌШєАбЁїADEШЦЕуAа§зЊЃЌЕБЁЯEACЃН90ЁуЪБЃЌжБНгаДГіPBЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮABCDжаЃЌABЃН1ЃЌADЃН2ЃЌЖЏЕуMЁЂNЗжБ№ДгЖЅЕуAЁЂBЭЌЪБГіЗЂЃЌЧвЗжБ№бизХADЁЂBAдЫЖЏЃЌЕуNЕФЫйЖШЪЧЕуMЕФ2БЖЃЌЕуNЕНДяЖЅЕуAЪБЃЌдђСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌСЌНгBMЁЂCNНЛгкЕуPЃЌЙ§ЕуPЗжБ№зїABЁЂADЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЁЂFЃЌдђЯпЖЮEFЕФзюаЁжЕЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() Љ1C.
Љ1C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛжЛВЛЭИУїДќзгжазАгаШ§жЛДѓаЁЁЂжЪЕиЖМЯрЭЌЕФаЁЧђЃЌЧђУцЩЯЗжБ№БъгаЪ§зж1ЁЂЉ2ЁЂ3ЃЌНСдШКѓЯШДгжаШЮвтУўГівЛИіаЁЧђЃЈВЛЗХЛиЃЉЃЌМЧЯТЪ§зжзїЮЊЕуAЕФКсзјБъЃЌдйДггрЯТЕФСНИіаЁЧђжаШЮвтУўГівЛИіаЁЧђЃЌМЧЯТЪ§зжзїЮЊЕуAЕФзнзјБъЃЎ
ЃЈ1ЃЉгУЛЪїзДЭМЛђСаБэЕШЗНЗЈСаГіЫљгаПЩФмГіЯжЕФНсЙћЃЛ
ЃЈ2ЃЉЧѓЕуAТфдкЕкЫФЯѓЯоЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBдкЗДБШР§КЏЪ§yЃН![]() (xЃО0)ЕФЭМЯѓЩЯЃЌЕуCЃЌDдкЗДБШР§КЏЪ§yЃН
(xЃО0)ЕФЭМЯѓЩЯЃЌЕуCЃЌDдкЗДБШР§КЏЪ§yЃН![]() (kЃО0)ЕФЭМЯѓЩЯЃЌACЁЮBDЁЮyжсЃЌвбжЊЕуAЃЌBЕФКсзјБъЗжБ№ЮЊ1ЃЌ2ЃЌЁїOACгыЁїABDЕФУцЛ§жЎКЭЮЊ
(kЃО0)ЕФЭМЯѓЩЯЃЌACЁЮBDЁЮyжсЃЌвбжЊЕуAЃЌBЕФКсзјБъЗжБ№ЮЊ1ЃЌ2ЃЌЁїOACгыЁїABDЕФУцЛ§жЎКЭЮЊ![]() ЃЌдђkЕФжЕЮЊ_____ЃЎ
ЃЌдђkЕФжЕЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНааЫФБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
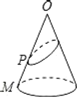
ЁОЬтФПЁПвбжЊЃКШчгвЭМЃЌOЮЊдВзЖЕФЖЅЕуЃЌMЮЊЕзУцдВжмЩЯвЛЕуЃЌЕуPдкOMЩЯЃЌвЛжЛТьвЯДгЕуPГіЗЂШЦдВзЖВрУцХРааЛиЕНЕуPЪБЫљОЙ§ЕФзюЖЬТЗОЖЕФКлМЃШчЭМЃЎШєбиOMНЋдВзЖВрУцМєПЊВЂеЙЦНЃЌЫљЕУВрУцеЙПЊЭМЪЧЃЈЁЁЁЁЃЉ
A.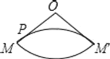 B.
B.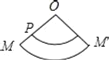
C.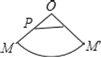 D.
D.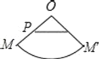
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com