【题目】如图，
内接于
，
，
是的直径，点
是延长线上一点，且
．
求证：
是的切线；
若
，求的直径．
【答案】（1）详见解析；（2）
的直径为
．
【解析】
（1）连接OA，根据圆周角定理首先求得∠AOC的度数，然后根据三角形内角和定理求得∠OAP=90°，从而求解；
（2）根据直角三角形的性质，直角三角形中30°所对的边等于斜边的一半，即可求解．
（1）连接OA．
∵∠B=60°，∴∠AOC=2∠B=120°，∠AOD=180°－120°=60°．
又∵OA=OC，∴∠OAC=∠OCA=30°．
又∵AP=AC，∴∠P=∠ACP=30°，∴∠OAP=180°－∠AOD﹣∠P=90°，∴OA⊥PA，∴PA是⊙O的切线．
（2）设该圆的半径为x．
在Rt△OAP中，∵∠P=30°，∴PO=2OA=OD+PD．
又∵OA=OD，∴1+x=2x，解得：x=1，∴OA=PD=1，所以⊙O的直径为2．
科目：初中数学 来源： 题型：
【题目】已知反比例函数
（k≠0）的图象经过点（1，﹣k+2）．
（1）求这个反比例函数的表达式；
（2）若（a，y1），（a+1，y2）是这个反比例函数图象上同一象限内的两个点，请比较y1、y2的大小，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，以
为边作等腰直角
，使
，边
交
于点
.
(1)如图1，过点
作
于点
，当
时，求线段
的长；
(2)如图2，过点
作
于点，且
，连接
， 若为的中点，求证：
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，有
两点，另有一次函数
的图象．
（1）若
，判断函数的图象与线段
是否有交点？请说明理由．
（2）当
时，函数图象与线段有交点，求k的取值范围．
（3）若
，求证：函数图象一定经过线段的中点．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，BE=3cm，AD=9cm．
求：（1）DE的长；
（2）若CE在△ABC的外部（如图），其它条件不变，DE的长是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板(AC＝BC，∠ACB＝90°)，点C在DE上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为______cm.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图矩形ABCD中，AB=3cm，AD=9cm，将此矩形折叠，使点B与点D重合，折痕为EF．
（1）求证：BE=BF；
（2）求△ABE的面积；
（3）求折痕EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠MON及其边上一点A，以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C，再以点C为圆心，AC长为半径画弧，恰好经过点B，错误的结论是（ ）.
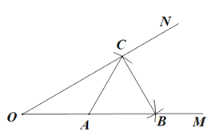
A.
B.∠OCB＝90°C.∠MON＝30°D.OC＝2BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
