
【题目】在![]() 中,
中,![]() ,以
,以![]() 为边作等腰直角
为边作等腰直角![]() ,使
,使![]() ,边
,边![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)如图2,过点![]() 作
作![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() , 若
, 若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() .
.

【答案】(1)![]() +1;(2)见解析;
+1;(2)见解析;
【解析】
(1)利用等腰直角![]() 求出BD=2
求出BD=2![]() ,∠ABD=45
,∠ABD=45![]() 得到AH=
得到AH=![]() ,∠HAD=45
,∠HAD=45![]() ,再由
,再由![]() ,
, ![]() 得到EC=BE,∠EAH=
得到EC=BE,∠EAH=![]() ,利用勾股定理求出HE,即可得到EC的长;
,利用勾股定理求出HE,即可得到EC的长;
(2)连接CD,利用SAS证明△ABF≌△DAC,得到AF=CD. 过点C作CH⊥AB,交BD于G,连接AG,通过证明△CGE≌△ADE证得四边形ADCG是平行四边形,得到AG=CD,
再根据![]() 得到AG=DG=BG,得到AF=CD=DG=2DE.
得到AG=DG=BG,得到AF=CD=DG=2DE.
(1)∵等腰直角![]() ,
,![]() ,
,![]() ,
,
∴∠ABD=45![]() ,AB=
,AB=![]() ,
,
∴BD=![]() ,
,
∵![]() ,
,
∴AH=![]() ,∠HAD=45
,∠HAD=45![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,∠DAC=15
,∠DAC=15![]() ,
,
∴![]() ,
,![]() ,∠EAH=
,∠EAH=![]() ,
,
∴∠C=∠EBC,
∴EC=BE
设HE=x,则AE=2x,
∵![]() ,
,
∴![]() ,
,
得x=1,∴HE=1,
∴EC=BE=BH+HE=![]() +1.
+1.
(2)连接CD,
∵AC=BC,
∴∠ABC=∠BAC,
∵![]() ,
,
∴∠FBC=![]() ,
,
∴∠FBA=∠CAD,
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AD,
∵AC=BC=FB,
∴△ABF≌△DAC,
∴AF=CD,
过点C作CH⊥AB,交BD于G,连接AG,
∴CH∥AD,
∴∠ACH=∠DAC,
∵∠CEG=∠AED,AE=CE,
∴△CGE≌△ADE,
∴CG=AD,GE=DE
∴四边形ADCG是平行四边形,
∴AG=CD,
∵AC=BC, CH⊥AB,
∴AH=BH,
∵CH∥AD,
∴![]() ,
,
∴BG=GD,
∴AG=BG=DG,
∴AG=2DE,
∴AF=CD=AG=2DE.



科目:初中数学 来源: 题型:
【题目】如图是某游泳馆的剖面图,运动员小亮站在![]() 米高的跳台上(即
米高的跳台上(即![]() ),目测游泳馆远处墙壁的最高点
),目测游泳馆远处墙壁的最高点![]() 的仰角为
的仰角为![]() ,已知
,已知![]() ,游泳馆的馆顶是一个弓形,且弓形高是
,游泳馆的馆顶是一个弓形,且弓形高是![]() .求该游泳馆的馆顶离地面的最大高度.(小亮的身高可忽略不计,结果精确到
.求该游泳馆的馆顶离地面的最大高度.(小亮的身高可忽略不计,结果精确到![]() 米).
米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=20°,点P在OA边上.
(1)以点O为圆心,OP长为半径作![]() ,交OB于点C;
,交OB于点C;
(2)分别以点P、C为圆心,PC长为半径作弧,交![]() 于点D、E;
于点D、E;
(3)连接DE,分别交OC、OP于点F、G;
(4)连接DP.
根据以上作图过程及所作图形,下列结中正确的是_____.(填序号)
①OC垂直平分DP;②∠COD=∠COP;③DF=FG;④OD=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】楼房AB后有一假山,其坡度为i=1:![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=30米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数是( )
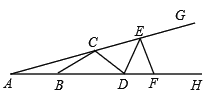
A. 80° B. 90° C. 100° D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线.求证:AD⊥BC.
(填空)

证明:∵AD是BC边上的中线
∴BD=CD(中线的意义)
在△ABD和△ACD中
∵ 
①________;②________;③________.
∴ ________≌ ________(________)
∴∠ADB=________(________)
∴∠ADB= ![]() ∠BDC=90°(平角的定义)
∠BDC=90°(平角的定义)
∴AD⊥BC(垂直的定义)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com