
【题目】如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD=![]() ,求∠BAC的度数;
,求∠BAC的度数;
(2)若点E为弧ADB的中点,连接OE,CE.求证:CE平分∠OCD.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,AB,AC为弦,且∠ADC=∠DAB+∠ACD,AB交CD于E点.
(1)求证:AB=AC.
(2)DF为切线,若DE=2,CE=10,求cos∠ADF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
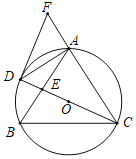
【题目】(问题探究)
(1)如图①,点E是正△ABC高AD上的一定点,请在AB上找一点F,使EF=![]() AE,并说明理由;
AE,并说明理由;
(2)如图②,点M是边长为2的正△ABC高AD上的一动点,求![]() AM+MC的最小值;
AM+MC的最小值;
(问题解决)
(3)如图③,A、B两地相距600km,AC是笔直地沿东西方向向两边延伸的一条铁路,点B到AC的最短距离为360km.今计划在铁路线AC上修一个中转站M,再在BM间修一条笔直的公路。如果同样的物资在每千米公路上的运费是铁路上的两倍。那么,为使通过铁路由A到M再通过公路由M到B的总运费达到最小值,请确定中转站M的位置,并求出AM的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)请直接写出不等式![]() 的解集;
的解集;
(2)将![]() 轴下方的图象沿
轴下方的图象沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用线段EG,FH将正方形ABCD按如图1所示的方式分割成4个全等的四边形,且AE=BF=CG=DH,tan∠HFC=2,再将这四个四边形按如图2所示的方式拼成一个大正方形IJKL,若设正方形ABCD的面积为S1,正方形IJKL的面积为S2.小四边形MNPQ的面积为8,则 ![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com