
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
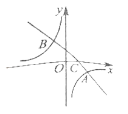
(1)请直接写出不等式![]() 的解集;
的解集;
(2)将![]() 轴下方的图象沿
轴下方的图象沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )
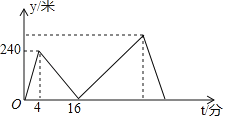
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O与AC相切于点E,交BC于点F,连接DF.
(1)求证:DF=2CE;
(2)若BC=3,sinB=![]() ,求线段BF的长.
,求线段BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
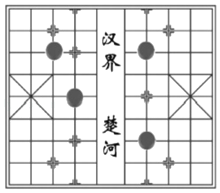
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD=![]() ,求∠BAC的度数;
,求∠BAC的度数;
(2)若点E为弧ADB的中点,连接OE,CE.求证:CE平分∠OCD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() .
.

(1)求该抛物线和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的动点,设
上方抛物线上的动点,设![]() 点的横坐标为
点的横坐标为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积,并求出
的面积,并求出![]() 面积的最大值;
面积的最大值;
(3)设P点是直线![]() 上一动点,
上一动点,![]() 为抛物线上的点,是否存在点
为抛物线上的点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、P、
、P、![]() 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点
为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点![]() 坐标,不存在说明理由.
坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
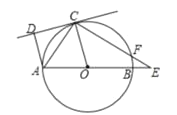
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
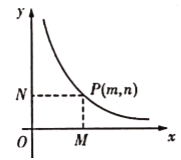
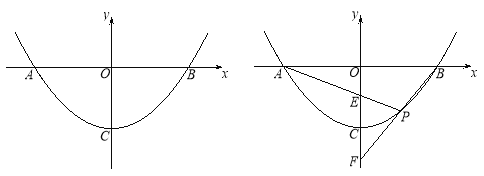
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P为抛物线上,且位于x轴下方.
(1)如图1,若P(1,-3)、B(4,0),
① 求该抛物线的解析式;
② 若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2) 如图2,已知直线PA、PB与y轴分别交于E、F两点.当点P运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com