
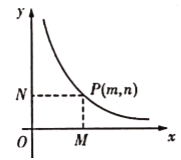
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意得![]() ,
,![]() ,故可得出k=
,故可得出k=![]() ;由
;由![]() 变形为
变形为![]() 得A,B两点为抛物线与x轴的交点,故点C为直角顶点,求出点C坐标,代入
得A,B两点为抛物线与x轴的交点,故点C为直角顶点,求出点C坐标,代入![]() ,求出a的值即可;
,求出a的值即可;
(2)由![]() 为正三角形可求出点C坐标,从而得出抛物线y2的解析式,再根据直线
为正三角形可求出点C坐标,从而得出抛物线y2的解析式,再根据直线![]() 平分
平分![]() 求出b和c,得到直线y3解析式,联立y1与y3,y2与y3,求出交点坐标,从而解决问题;
求出b和c,得到直线y3解析式,联立y1与y3,y2与y3,求出交点坐标,从而解决问题;
(3)分![]() 、
、![]() 、
、![]() 、
、![]() ,四种情况分别求解即可.
,四种情况分别求解即可.
(1)∵点![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,
,![]()
又双曲线![]() 经过点
经过点![]()
∴![]() ;
;
∵![]()
∴抛物线y1与x轴的交点坐标为(-1,0),(3,0)
∴点![]() 在抛物线y1上,
在抛物线y1上,
∴点C是直角顶点,AB=3-(-1)=4,
过点C作CD⊥AB于点D,则CD=![]() AB=2,
AB=2,
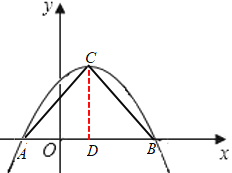
∴OD=AD-AO=1,
∴C(1,2)
把C(1,2)代入![]() ,求得,
,求得,![]()
∴![]()
![]() ;
;
![]() ∵A(-1,0),B(3,0)
∵A(-1,0),B(3,0)
∴AB=4
过C点作CD⊥AB,垂足为D,
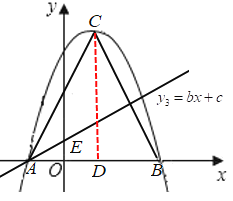
∵△ABC是正三角形,
∴AC=AB=4,AD=![]() AB=2,OD=1
AB=2,OD=1
∴![]()
∴C(1,![]() )
)
把C(1,![]() ) 代入
) 代入![]() ,解得,
,解得,![]() ,
,
∴![]()
∵直线![]() 平分
平分![]() ,
,
∴∠OAE=30°,
∴AE=2OE
∵AO=1,
∴![]() ,解得,
,解得,![]()
∴c=![]()
把(-1,0)代入![]() 得,b=
得,b=![]()
∴![]()
联立![]() 与
与![]() 得
得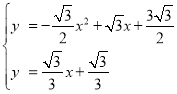
解得,![]() ,
,![]()
所以当![]() 时,
时,![]()
联立![]() 与
与![]() 得
得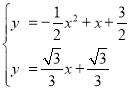 ,
,
解得,![]() ,
,![]()
当![]() 时,
时,![]()
所以当![]() 时,
时,![]()
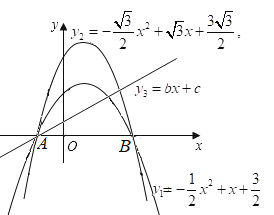
![]() ①当
①当![]() 时,
时,
抛物线![]() 与双曲线
与双曲线![]() 没有公共点;
没有公共点;
②当![]() 时,抛物线
时,抛物线![]() 与双曲线
与双曲线![]() 有唯一公共点
有唯一公共点
③当![]() 时,当抛物线右端点
时,当抛物线右端点![]() 正好落在双曲线上时,
正好落在双曲线上时,![]()
![]() 当
当![]() 时,抛物线
时,抛物线![]() 与双曲线
与双曲线![]() 有两个公共点;
有两个公共点;
④当![]() 时,抛物线
时,抛物线![]() 和双曲线
和双曲线![]() 始终有一个公共点;
始终有一个公共点;
所以当![]() 时,抛物线
时,抛物线![]() 和双曲线
和双曲线![]() 始终有一个公共点
始终有一个公共点


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“端午”节前,小明爸爸去超市购买了大小、形状、重量等都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时从盒中随机取出火腿粽子的概率为![]() ;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为
;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为![]() .
.
(1)请你用所学知识计算:爸爸买的火腿粽子和豆沙粽子各有多少只;
(2)若小明一次从盒内剩余粽子中任取2只,问恰有火腿粽子、豆沙粽子各1只的概率是多少.(用列表法或树状图计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
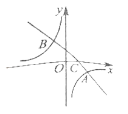
(1)请直接写出不等式![]() 的解集;
的解集;
(2)将![]() 轴下方的图象沿
轴下方的图象沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,![]() .
.
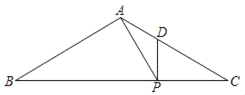
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用线段EG,FH将正方形ABCD按如图1所示的方式分割成4个全等的四边形,且AE=BF=CG=DH,tan∠HFC=2,再将这四个四边形按如图2所示的方式拼成一个大正方形IJKL,若设正方形ABCD的面积为S1,正方形IJKL的面积为S2.小四边形MNPQ的面积为8,则 ![]() 的值为( )
的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
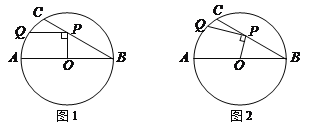
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com