
【题目】如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P,![]() .
.
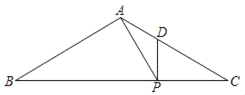
(1)求证:∠APD=∠C;
(2)如果AB=3,DC=2,求AP的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
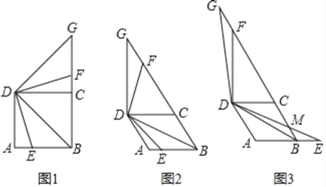
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.
①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
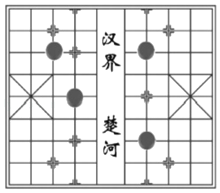
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() .
.

(1)求该抛物线和直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的动点,设
上方抛物线上的动点,设![]() 点的横坐标为
点的横坐标为![]() ,试用含
,试用含![]() 的代数式表示
的代数式表示![]() 的面积,并求出
的面积,并求出![]() 面积的最大值;
面积的最大值;
(3)设P点是直线![]() 上一动点,
上一动点,![]() 为抛物线上的点,是否存在点
为抛物线上的点,是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、P、
、P、![]() 为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点
为顶点的四边形为平行四边形,若存在,请直接写出符合条件的所有点![]() 坐标,不存在说明理由.
坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,已知
轴上,已知![]() ,抛物线
,抛物线![]() (其中
(其中![]() )经过
)经过![]() 三点,双曲线
三点,双曲线![]() (其中
(其中![]() )经过点
)经过点![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 且
且![]()
(1)求出![]() 的值;当
的值;当![]() 为直角三角形时,请求出
为直角三角形时,请求出![]() 的表达式;
的表达式;
(2)当![]() 为正三角形时,直线
为正三角形时,直线![]() 平分
平分![]() ,求
,求![]() 时
时![]() 的取值范围;
的取值范围;
(3)抛物线![]() (其中
(其中![]() )有一时刻恰好经过
)有一时刻恰好经过![]() 点,且此时抛物线与双曲线
点,且此时抛物线与双曲线![]() (其中
(其中![]() )有且只有一个公共点
)有且只有一个公共点![]() (其中
(其中![]() ),我们不妨把此时刻的
),我们不妨把此时刻的![]() 记作
记作![]() ,请直接写出抛物线
,请直接写出抛物线![]() (其中
(其中![]() )与双曲线
)与双曲线![]() (其中
(其中![]() )有一个公共点时
)有一个公共点时![]() 的取值范围.(
的取值范围.(![]() 是已知数)
是已知数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角度数为α,看这栋楼底部C处的俯角度数为β,热气球A处与楼的水平距离为100m,则这栋楼的高度表示为( )
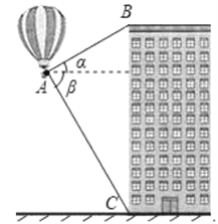
A.100(tanα+tanβ)mB.100(sinα+sinβ)mC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
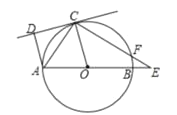
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月5日,我校组织全体学生参加了“走出校门,服务社会”的活动.九年级三班同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图.请根据同学所作的两个图形.解答:
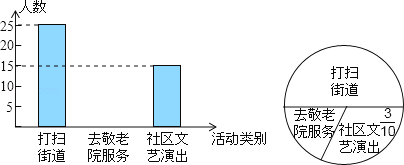
(1)九年级三班有多少名学生;
(2)补全直方图的空缺部分;
(3)若九年级有800名学生,估计该年级去敬老院的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线,![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且抛物线
,且抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
(1)抛物线的表达式;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于直线
关于直线![]() 对称,抛物线
对称,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),要使
左侧),要使![]() ,求所有满足条件的抛物线
,求所有满足条件的抛物线![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com