
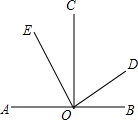
 如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°.
如图,CO⊥AB,垂足为O,∠COE-∠BOD=4°,∠AOE+∠COD=116°,则∠AOD=150°. 分析 根据垂直可得∠AOC=∠BOC=90°,从而可得∠AOE=90°-∠EOC,∠COD=90°-∠BOD,再代入∠AOE+∠COD=116°可得∠EOC+∠BOD=64°,再和∠COE-∠BOD=4°组成方程组,再解可得∠BOD的度数,进而可得∠AOD的度数.
解答 解:∵CO⊥AB,
∴∠AOC=∠BOC=90°,
∴∠AOE=90°-∠EOC,
∠COD=90°-∠BOD,
∵∠AOE+∠COD=116°,
∴90°-∠EOC+90°-∠BOD=116°,
∴∠EOC+∠BOD=64°,
∵∠COE-∠BOD=4°,
∴$\left\{\begin{array}{l}{∠EOC+∠BOD=64°}\\{∠COE-∠BOD=4°}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{∠COE=34°}\\{∠BOD=30°}\end{array}\right.$,
∴∠AOD=150°,
故答案为:150.
点评 此题主要考查了垂直,以及角的计算,关键是正确理清角之间的关系,得到∠EOC+∠BOD=64°.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
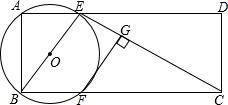 如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.
如图,在矩形ABCD中,AB=2,AD=5,过点A、B作⊙O,交AD、BC于点E、F,连接BE、CE,过点F作FG⊥CE,垂足为G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
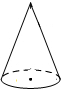 如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )
如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为α,则( )| A. | 圆锥的底面半径为3 | B. | tanα=$\frac{\sqrt{2}}{2}$ | ||
| C. | 圆锥的表面积为12π | D. | 该圆锥的主视图的面积为8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
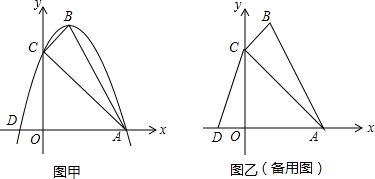
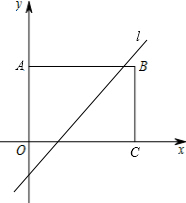 如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.
如图,矩形OABC中,A、C分别是y轴、x轴上的点,且OA=3,OC=4,将矩形OABC沿直线l折叠,使A点与C点重合,则直线l的解析式为y=$\frac{4}{3}x$-$\frac{7}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com