
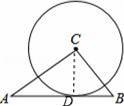
如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )


A.2.3 B.2.4 C.2.5 D.2.6
B【考点】切线的性质;勾股定理的逆定理.
【分析】首先根据题意作图,由AB是⊙C的切线,即可得CD⊥AB,又由在直角△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理求得AB的长,然后由S△ABC=
 AC•BC=
AC•BC=
 AB•CD,即可求得以C为圆心与AB相切的圆的半径的长.
AB•CD,即可求得以C为圆心与AB相切的圆的半径的长.
【解答】解:在△ABC中,
∵AB=5,BC=3,AC=4,
∴AC2+BC2=32+42=52=AB2,
∴∠C=90°,
如图:设切点为D,连接CD,
∵AB是⊙C的切线,
∴CD⊥AB,
∵S△ABC=
 AC•BC=
AC•BC=
 AB•CD,
AB•CD,
∴AC•BC=AB•CD,
即CD=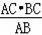
 =
=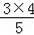
 =
=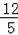
 ,
,
∴⊙C的半径为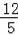
 ,
,
故选B.

【点评】此题考查了圆的切线的性质,勾股定理,以及直角三角形斜边上的高的求解方法.此题难度不大,解题的关键是注意辅助线的作法与数形结合思想的应用.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:
如图,在半径为6cm的⊙O中,点A是劣弧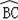
 的中点,点D是优弧
的中点,点D是优弧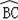
 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6
 ;③sin∠AOB=
;③sin∠AOB=
 ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )


A.①③ B.①②③④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
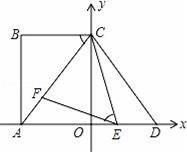
如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=
 ,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,∠CDE=∠CAO,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)求AC的长和点D的坐标;
(2)证明:△AEF∽△DCE;
(3)当△EFC为等腰三角形时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,直线
 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥OC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥OC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1= 
 ,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于 .
,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于 .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com